(C4) Геометрическая задача на вычисление
Задание 4213
В прямоугольном треугольнике $$ABC$$ из вершины прямого угла $$B$$ проведены медиана $$BE$$ и высота $$BK$$. Найдите длину гипотенузы $$AC$$, если $$KE=1$$, $$\angle BAK=60^{\circ}$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 2445
В прямоугольном треугольнике $$ABC$$ с прямым углом $$C$$ известны катеты: $$AC=6$$, $$BC=8$$ . Найдите медиану $$CK$$ этого треугольника.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 3335
В прямоугольном треугольнике, периметр которого равен $$36$$ см, вписана окружность. Гипотенуза делится точкой касания в отношении $$2:3$$. Найдите длину гипотенузы.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
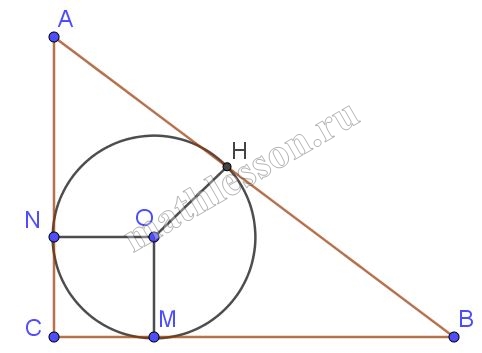
1) Пусть $$\frac{AH}{HB}=\frac{2}{3}$$, тогда AH=2x; HB=3x
2) По свойству касательных MB=HB=3x, NA=AH=2x
3) Пусть ON=OH=OM=y, но NC=CM=y. Тогда по т. Пифагора :$$(y+2x)^{2}+(y+3x)^{2}=(5x)^{2}(1)$$
4) т.к. P=36, то $$y+2x+y+3x+5x=36$$, $$2y=36-10x\Leftrightarrow y=18-5x$$
Подставим в (1)
$$(18-5x+2x)^{2}+(18-5x+3x)^{2}=25x^{2}$$
$$324-108x+9x^{2}+324-72x+4x^{2}=25x^{2}$$
$$12x^{2}+180x-648=0$$
$$x^{2}+15x-54=0$$
$$\left\{\begin{matrix}x_{1}+x_{2}=-15\\x_{1}*x_{2}=-54\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}x_{1}=3\\x_{2}=-18\end{matrix}\right.$$
-18 не может быть, так как длина - число положительное, следовательно, $$5x=5*3=15$$ - длина гипотенузы
Задание 4155
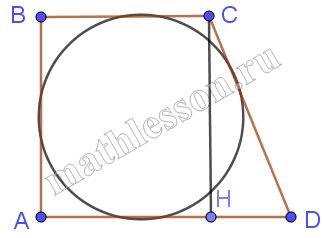
В прямоугольную трапецию вписана окружность. Найдите её радиус, если основания трапеции $$2$$ см и $$3$$ см.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
1) Пусть К - точка каасния АВ и окружности
2) Пусть r - радиус окружности $$BK=KA=r$$ $$\Rightarrow$$ $$BA=2r$$
3) По свойству описанного четырехугольника: $$AB+CD=BC+AD$$ $$\Rightarrow$$
$$2r+CD=2+3=5$$ $$\Rightarrow$$
$$CD=5-2R$$
4) Опустим $$CC_{1}\perp AD$$ $$\Rightarrow$$
$$CC_{1}=AB=2r$$
По теореме Пифагора: $$CC_{1}^{2}+C_{1}D^{2}=CD^{2}$$
$$C_{1}D=AD-BC=3-2=1$$
$$(2r)^{2}+1^{2}=(5-2r)^{2}$$
$$4r^{2}+1=25-20r+4r^{2}$$
$$20r=24$$ $$\Rightarrow$$ $$r=1,2$$
Задание 3476
В прямоугольную трапецию с основаниями $$5$$ см и $$6$$ см вписана окружность. Найдите площадь этой трапеции.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
1) BC=5; CD=6; опустим $$CH\perp AD$$ , тогда $$HD=6-5=1$$.
2) Пусть AB=x, тогда CH=x Пусть CD=y , тогда из $$\Delta CHD: x^{2}+1^{2}=y^{2}$$
По свойству описанного многоугольника : $$5+6=x+y$$. Тогда:
$$\left\{\begin{matrix}x^{2} +1=y^{2}\\x+y-11 & &\end{matrix}\right.\Leftrightarrow$$$$ \left\{\begin{matrix}x^{2}+1=(11-x)^{2} \\y=11-x\end{matrix}\right.$$
3)$$S=\frac{5+6}{2}*\frac{60}{11}=30$$.
Задание 252
В равнобедренной трапеции $$ABCD$$ с большим основанием $$AD$$ биссектриса угла $$A$$ пересекается с биссектрисой угла $$C$$ в точке $$F$$, а также пересекает сторону $$CD$$ в точке $$K$$. Известно, что угол $$AFC$$ равен $$150^{\circ}$$. Найдите $$FK$$, если $$CF=12\sqrt{3}$$.
Задание 4135
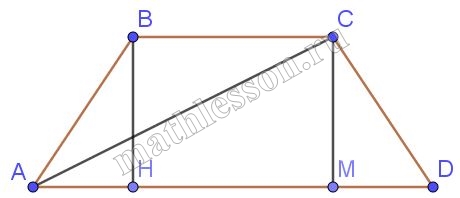
В равнобедренной трапеции диагональ длиной $$3$$ см образует угол $$45^{\circ}$$ с основанием. Найдите площадь трапеции.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
1) Построим BH и CM $$\perp AD\Rightarrow$$
$$\bigtriangleup BHD$$ - прямоугольный
$$\angle HDB=45^{\circ}\Rightarrow$$ ; $$\angle HBD=45^{\circ}\Rightarrow$$
$$BH=HD=x$$
$$BH^{2}+HD^{2}=BD^{2}$$
$$2x^{2}=9\Rightarrow x^{2}=\frac{9}{2}$$ $$\Rightarrow$$
$$x=\frac{3\sqrt{2}}{2}$$
2) $$BH=CM;AB=CD\Rightarrow$$
$$\bigtriangleup AHB=\bigtriangleup CMD$$ $$\Rightarrow$$
$$AH=MD=y$$ $$\Rightarrow$$
$$HM=\frac{3\sqrt{2}}{2}-y=BC$$
3) $$S_{ABCD}=\frac{AD+BC}{2}\cdot BH=$$
$$=\frac{y+\frac{3\sqrt{2}}{2}+\frac{3\sqrt{2}}{2}-y}{2}\cdot\frac{3\sqrt{2}}{2}=$$
$$=\frac{3\sqrt{2}}{2}\cdot\frac{3\sqrt{2}}{2}=\frac{9}{2}=4,5$$
Задание 4030
В равнобедренной трапеции основания равны $$12$$ см и $$20$$ см, а диагонали взаимно перпендикулярны. Найдите площадь трапеции.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 3289
В равнобедренной трапеции с основаниями $$10$$ и $$26$$ см диагональ является биссектрисой острого угла. Найдите площадь трапеции.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
1) $$\angle BAC=\angle CAD$$ (AC-бисссектриса), $$\angle CAD=\angle BCA$$ ( накрест лежащие ), тогда $$\angle BAC=\angle ACA$$, следовательно, $$\Delta ABC$$ - равнобедренный, и AB=BC=10
2) Пусть BH=CM - высота, тогда $$AH=MD=\frac{AD-BC}{2}=8$$
3) из $$\Delta ABH:$$ $$BH=\sqrt{AB^{2}-AB^{2}}=6$$
4) $$S_{ABCD}=\frac{10+26}{2}*6=108$$
Задание 2682
В равнобедренном треугольнике $$ABC$$ основание $$AC$$ равно $$6$$ см, а высота опущенная на основание равна $$4$$ см. Найдите периметр треугольника $$CHB$$, где $$CH$$ – высота, опущенная на боковую сторону.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 4259
В равнобедренном треугольнике с основанием $$AC$$ и боковой стороной $$AB$$ проведена высота $$AD$$ делящая боковую сторону $$BC$$ в отношении $$BD:DC=7:1$$. Найдите $$AB$$ если $$AC=4$$ см.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 2881
В равнобедренном треугольнике с углом $$45^{\circ}$$ при основании вписан квадрат так, что одна из его сторон лежит на основании треугольника. Найдите площадь квадрата, если площадь треугольника равна $$18$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 3311
В равнобедренную трапецию $$ABCD$$ с основаниями $$BC=18$$ и $$AD=32$$ вписан круг. Найдите площадь трапеции.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
1) $$BC+AD=AB+CD=18+32=50$$ ( по свойству описанного четырехугольника ), тогда AB=CD=25
2) Пусть $$BH\left | \right |CM \perp AD$$, тогда $$AH=MD=\frac{AD-BC}{2}=7$$
3) По т. Пифагора $$\Delta ABH$$: $$BH=\sqrt{25^{2}-7^{2}}=24$$
4) $$S=\frac{18+32}{2}*24=600$$
Задание 2978
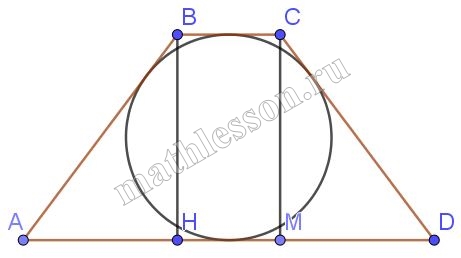
В равнобедренную трапецию вписана окружность радиуса $$2$$ см. Найдите площадь трапеции, если длина боковой стороны равна $$10$$ см
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
1) Пусть O-центр окружности, $$OH\perp BC$$ и $$OM\perp AD$$ (радиусы в точки касания )$$\Rightarrow$$ $$HK=2+2=4$$. Пусть $$CK\left | \right |HM\Rightarrow$$ $$CK=4$$
2) По свойству описанного четырехугольника : $$AB+CD=BC+AD=20$$
3) $$S_{ABCD}=\frac{BC+AD}{2}*CK=\frac{20}{2}*4=40$$