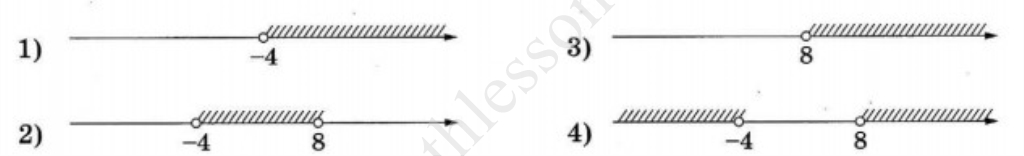ОГЭ 2021. Вариант 2. Ященко 36 вариантов ФИПИ школе.
Решаем 2 вариант ОГЭ Ященко 2021 года сборника ФИПИ школе 36 вариантов. Полный разбор всего 2 варианта (всех заданий).
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 1-5
Зонты
Две подруги Оля и Аня задумались о том, как рассчитать площадь поверхности зонта.
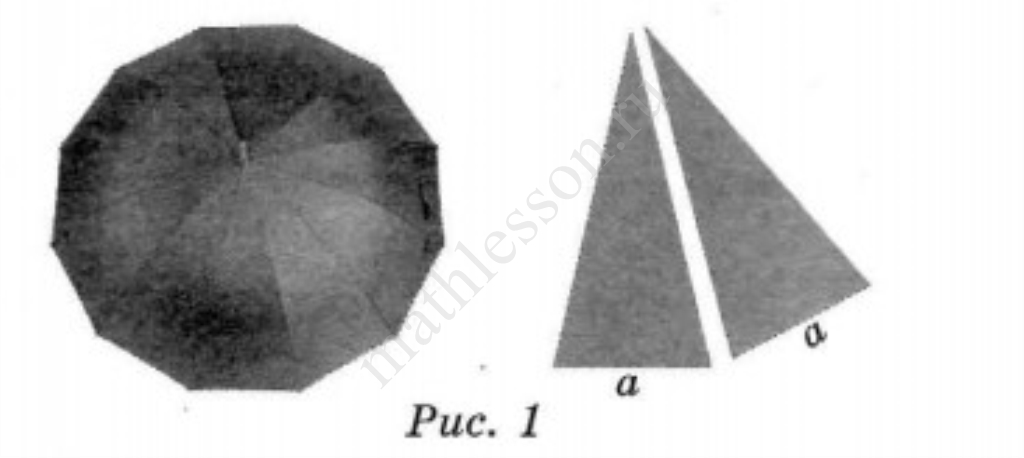
На первый взгляд зонт кажется круглым, а его купол напоминает часть сферы (сферический сегмент). Но если присмотреться, то видно, что купол зонта состоит из двенадцати отдельных клиньев, натянутых на каркас из двенадцати спиц (рис. 1). Сферическая форма в раскрытом состоянии достигается за счёт гибкости спиц и эластичности ткани, из которой изготовлен зонт.
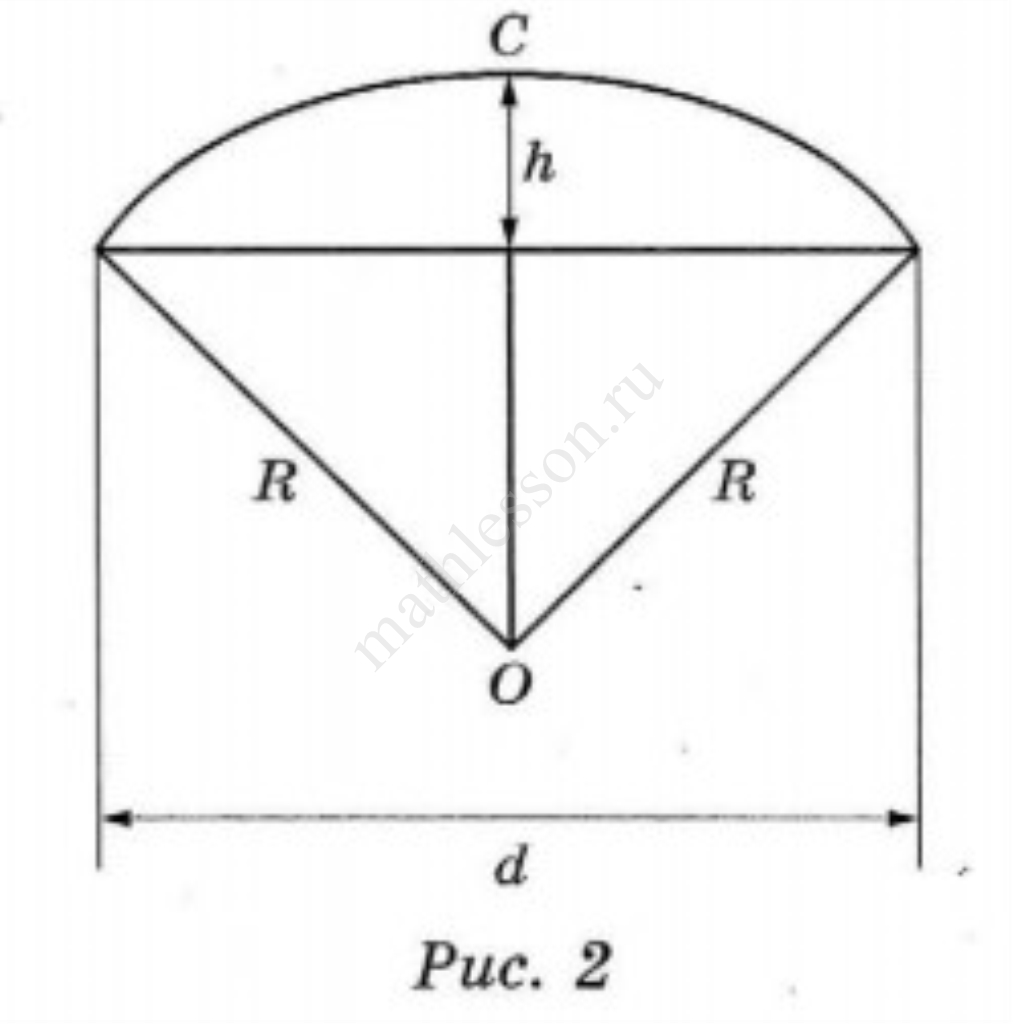
Оля и Аня сумели измерить расстояние между концами соседних спиц $$a$$. Оно оказалось равно $$28$$ см. Высота купола зонта $$h$$ (рис. 2) оказалась равна $$27$$ см, а расстояние $$d$$ между концами спин, образующих дугу окружности, проходящей через вершину зонта, — ровно $$108$$ см.
- Длина зонта в сложенном виде равна $$27$$ см и складывается из длины ручки (рис. 3) и трети длины спицы (зонт в три сложения). Найдите длину спицы, если длина ручки зонта равна $$6,8$$ см.
- Поскольку зонт сшит из треугольников, рассуждала Оля, площадь его поверхности можно найти как сумму площадей треугольников. Вычислите площадь поверхности зонта методом Оли, если высота каждого равнобедренного треугольника, проведённая к основанию, равна $$59$$ см. Ответ дайте в квадратных сантиметрах с округлением до десятков.
- Аня предположила, что купол зонта имеет форму сферического сегмента. Вычислите радиус $$R$$ сферы купола, зная, что $$OC = R$$ (рис. 2). Ответ дайте в сантиметрах.
- Аня нашла площадь купола зонта как площадь поверхности сферического сегмента по формуле $$S = 2\pi Rh$$, где R — радиус сферы, a h — высота сегмента. Рассчитайте площадь поверхности купола способом Ани. Число $$\pi$$ округлите до $$3,14$$. Ответ дайте в квадратных сантиметрах с округлением до целого.
- Рулон ткани имеет длину $$20$$ м и ширину $$90$$ см. На фабрике из этого рулона были вырезаны треугольные клинья для $$15$$ зонтов, таких же, как зонт, который был у Оли и Ани. Каждый треугольник с учётом припуска на швы имеет площадь $$850$$ кв. см. Оставшаяся ткань пошла в обрезки. Сколько процентов ткани рулона пошло в обрезки?
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
1) Длина $$\frac{1}{3}$$ спицы: $$27-6,8=20,2$$ см. Тогда длина всей спицы: $$3\cdot 20,2=60,6$$ см.
2) Площадь одного треугольника: $$S_1=\frac{1}{2}\cdot 28\cdot 59=826$$. Тогда площадь поверхности зонта: $$S_2=12\cdot 826=9912\approx 9910$$ см$$^2$$.
3) Пусть $$OM=x$$; из $$\triangle OLN: OM$$ - высота и медиана $$\to MN=\frac{d}{2}=54$$ см. Из $$\triangle OMN: OM^2+MN^2=ON^2\to x^2+54^2=(x+27)^2\leftrightarrow 54^2=54x+27^2\leftrightarrow$$ $$\leftrightarrow 54x=2916-729\to x=40,5\to R=40,5+27=67,5$$ см.
4) $$S=2\cdot 3,14\cdot 67,5\cdot 27=11445,3\approx 11445$$ см$$^2$$.
5) Количество клиньев: $$15\cdot 12=180$$ шт. Площадь клиньев: $$\frac{180\cdot 850}{100\cdot 100}=15,3$$ м$$^2$$. Площадь рулона: $$20\cdot 0,9=18$$ м$$^2$$. Обрезков: $$18-15,3=2,7$$ м$$^2$$. В процентах $$\frac{2,7}{18}\cdot 100=15%$$
Задание 7
Одно из чисел $$\sqrt{29}$$, $$\sqrt{34}$$, $$\sqrt{39}$$, $$\sqrt{45}$$ отмечено на прямой точкой $$A$$. Какое это число?
1) $$\sqrt{29}$$
2) $$\sqrt{34}$$
3) $$\sqrt{39}$$
4) $$\sqrt{45}$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 8
Найдите значение выражения $$\frac{(b^{-5})^2}{b^{-12}}$$ при $$b = 5$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
$$(x+2)^2=(1-x)^2$$ из этого получаем 2 уравнения:
1) $$x+2=1-x\to 2x=-1\to x=-0,5$$
2) $$x+2=x-1\to$$ корней нет
Задание 10
В магазине канцтоваров продаётся $$120$$ ручек: $$32$$ — красные, $$32$$ — зелёные, $$46$$ — фиолетовые, остальные — синие и чёрные, их поровну. Найдите вероятность того, что случайно выбранная в этом магазине ручка будет красной или фиолетовой.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 11
Установите соответствие между формулами, которыми заданы функции, и графиками этих функций.
ГРАФИКИ
Формулы:
А) $$y = x^2 + 8x + 12$$
Б) $$y = x^2 - 8x + 12$$
В) $$y = -x^2 + 8x - 12$$
| А | Б | В |
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
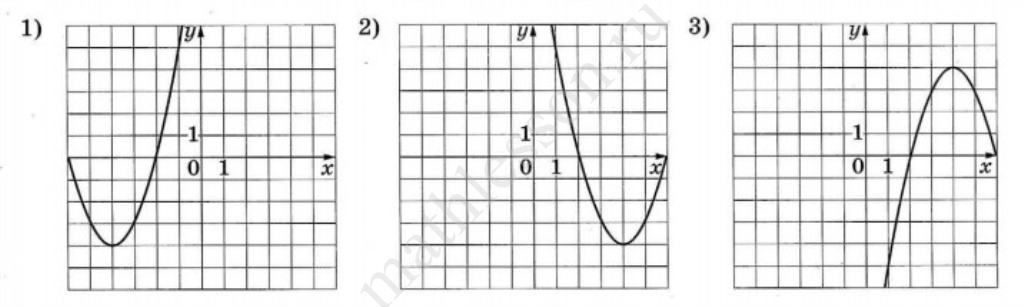
У 3-го ветви направлены вниз, значит $$a<0 (y=ax^2+bx+c)\to B.$$
Найдем абсциссу вершины для A: $$x_0=-\frac{8}{2}=-4\to$$ 1 график. Тогда 123.
Задание 12
Центростремительное ускорение при движении по окружности (в м/с²) вычисляется по формуле $$a = \omega^2 R$$, где $$\omega$$ — угловая скорость (в с⁻¹), $$R$$ — радиус окружности (в метрах). Пользуясь этой формулой, найдите радиус $$R$$, если угловая скорость равна $$7,5$$ с⁻¹, а центростремительное ускорение равно $$337,5$$ м/с². Ответ дайте в метрах.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 14
В течение $$20$$ банковских дней акции компании дорожали ежедневно на одну и ту же сумму. Сколько стоила акция компании в последний день этого периода, если в $$9$$-й день акция стоила $$555$$ рублей, а в $$13$$-й день — $$631$$ рубль?
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 15
Сторона треугольника равна $$16$$, а высота, проведённая к этой стороне, равна $$27$$. Найдите площадь этого треугольника.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 16
Четырёхугольник $$ABCD$$ вписан в окружность. Угол $$ABC$$ равен $$92^\circ$$, угол $$CAD$$ равен $$60^\circ$$. Найдите угол $$ABD$$. Ответ дайте в градусах.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 17
Диагональ прямоугольника образует угол $$63^\circ$$ с одной из его сторон. Найдите острый угол между диагоналями этого прямоугольника.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 18
На клетчатой бумаге с размером клетки $$1 \times 1$$ изображена трапеция. Найдите её площадь.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 19
Какие из следующих утверждений верны?
- Касательная к окружности параллельна радиусу, проведённому в точку касания.
- Если в ромбе один из углов равен $$90^{\circ}$$ градусам, то этот ромб является квадратом.
- Сумма углов равнобедренного треугольника равна $$180^{\circ}$$ градусам.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
1) нет, перпендикулярна
2) да
3) да (любого треугольника)
Задание 20
Решите уравнение: $$x^6 = -(7x + 10)^3$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
$$x^6=-(7x+10)^3\leftrightarrow x^2=-(7x-10)\leftrightarrow x^2+7x+10=0.$$ Из этого получаем два уравнения:
1) $$x_1+x_2=-7\to x_1=-2$$
2) $$x_1\cdot x_2=10\to x_2=-5$$
Задание 21
Два велосипедиста одновременно отправились в $$224$$ - километровый пробег. Первый ехал со скоростью, на $$2$$ км/ч большей, чем скорость второго, и прибыл к финишу на $$2$$ час раньше второго. Найдите скорость велосипедиста, пришедшего к финишу вторым. Ответ дайте в км/ч.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Пусть x км/ч - скорость второго, тогда $$x+2$$ км/ч - скорость первого. Получим: $$\frac{224}{x}-\frac{222}{x+2}=2\leftrightarrow 112(x+2)-112x=1(x^2+2x)\leftrightarrow$$ $$\leftrightarrow 112x+224-112x=x^2+2x\leftrightarrow x^2+2x-224=0$$
Решаем по теореме Виета:
1) $$x_1+x_2=-2\to x_1=-16<0$$
2) $$x_1x_2=-224\to x_2=14$$ - ответ.
Задание 22
Постройте график функции $$y = x^2 - 3|x| - x$$ и определите, при каких значениях $$m$$ прямая $$y = m$$ имеет с графиком не менее одной, но не более трёх общих точек.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
$$y=x^2-3|x|-x$$ получаем уравнения:
1) $$y=x^2-3x-x, x\geq 0 \to y=x^2-4x, x\geq 0 (1)$$
2) $$y=x^2+3x-x, x<0 \to y=x^2+2x, x<0 (2)$$
(1) $$x_0=-\frac{-4}{2}=2; y_0=2^2-4\cdot 2=-4.$$ Нули функции: $$x^2-4x=0\to x_1=0; x_2=4.$$
(2) $$x_0=-\frac{2}{2}=-1; y_0=(-1)^2+2(-1)=-1.$$ Нули функции: $$x^2+2x=0\to x_1=0; x_2=-2.$$
Построим график функции: $$y=m$$ - прямая, параллельная Ox от одной до трех точек пересечения имеет при $$m\in[-4;-1]\cup[0;+\infty)$$
Задание 23
Вершины треугольника делят описанную около него окружность на три дуги, длины которых относятся как $$6:11:19$$. Найдите радиус окружности, если меньшая из сторон равна $$15$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
1) Углы A,B,C - вписанные, потому равны половинам соответствующих дуг, потому отношение углов 6:11:29.
2) Т.к. $$\angle A+\angle B+\angle C=180^{\circ},$$ если $$\angle A=6x,$$ то: $$6x+11x+29x=180^{\circ}\to x=5\to \angle A=30^{\circ}.$$
3) Напротив меньшей стороны лежит меньший угол $$\to BC=15. R=\frac{a}{2\sin{\alpha}}=\frac{BC}{2\sin{A}}=\frac{15}{2\cdot \frac{1}{2}}=15$$
Задание 25
В треугольнике $$ABC$$ на его медиане $$BM$$ отмечена точка $$K$$ так, что $$BK:KM=4:9$$. Прямая $$AK$$ пересекает сторону $$BC$$ в точке $$P$$. Найдите отношение площади треугольника $$AKM$$ к площади треугольника $$KPCM$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
1) Пусть $$S_{ABC}=S\to S_{ABM}=S_{BMC}=\frac{S}{2}.$$
2) $$\frac{S_{ABK}}{S_{AKM}}=\frac{BK}{KM}=\frac{4}{9}\to S_{AKM}=\frac{9}{13}S_{ABM}\frac{9}{13}\cdot \frac{S}{2}=\frac{9S}{26}.$$
3) Пусть $$ML\parallel AP\to ML$$ - средняя линия $$\triangle APL$$ и $$PL=LC.$$ Но $$KP\parallel ML\to \frac{BK}{KM}=\frac{BP}{PL}=\frac{4}{9},$$ тогда $$\frac{BP}{PC}=\frac{4}{18}.$$
4) $$\frac{S_{APC}}{S_{ABC}}=\frac{PC}{BC}=\frac{18}{22}\to S_{APC}=\frac{9}{11}S\to S_{KPOM}=S_{APC}-S_{AKM}=\frac{9S}{11}-\frac{9S}{26}=$$ $$=\frac{9S(26-11)}{26\cdot 11}=\frac{15\cdot 9S}{26\cdot 11}\to \frac{S_{AKM}}{S_{KPCM}}=\frac{9}{26}\cdot \frac{26\cdot 11}{15\cdot 9}=\frac{11}{15}.$$