Задание 620
Задание 620
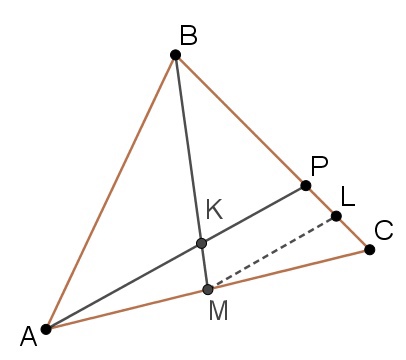
В треугольнике $$ABC$$ на его медиане $$BM$$ отмечена точка $$K$$ так, что $$BK:KM=4:1$$. Прямая $$AK$$ пересекает сторону $$BC$$ в точке $$P$$. Найдите отношение площади треугольника $$BKP$$ к площади треугольника $$ABC$$.
1) Пусть $$S_{ABC}=S$$. Тогда $$S_{ABM}=S_{BMC}=\frac{S}{2}$$.
2) Пусть $$ML||KP$$. По теореме Фалеса: $$\frac{AM}{MC}=\frac{PL}{LC}=\frac{1}{1}$$; $$\frac{BK}{KM}=\frac{BP}{PL}=\frac{4}{1}$$.
Тогда $$\frac{BP}{BC}=\frac{4}{6}=\frac{2}{3}$$.
3) $$\frac{S_{BKP}}{S_{BMC}}=\frac{BK\cdot BP}{BM\cdot BC}=\frac{4\cdot2}{5\cdot3}=\frac{8}{15}\Rightarrow S_{BKP}=\frac{8}{15}\cdot\frac{S}{2}=\frac{4}{15}S\Rightarrow\frac{S_{BKP}}{S_{ABC}}=\frac{4}{15}$$
Задание 1971
В треугольнике $$ABC$$ на его медиане $$BM$$ отмечена точка $$K$$ так, что $$BK:KM=4:9$$. Прямая $$AK$$ пересекает сторону $$BC$$ в точке $$P$$. Найдите отношение площади треугольника $$AKM$$ к площади треугольника $$KPCM$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


1) Пусть $$S_{ABC}=S\to S_{ABM}=S_{BMC}=\frac{S}{2}.$$
2) $$\frac{S_{ABK}}{S_{AKM}}=\frac{BK}{KM}=\frac{4}{9}\to S_{AKM}=\frac{9}{13}S_{ABM}\frac{9}{13}\cdot \frac{S}{2}=\frac{9S}{26}.$$
3) Пусть $$ML\parallel AP\to ML$$ - средняя линия $$\triangle APL$$ и $$PL=LC.$$ Но $$KP\parallel ML\to \frac{BK}{KM}=\frac{BP}{PL}=\frac{4}{9},$$ тогда $$\frac{BP}{PC}=\frac{4}{18}.$$
4) $$\frac{S_{APC}}{S_{ABC}}=\frac{PC}{BC}=\frac{18}{22}\to S_{APC}=\frac{9}{11}S\to S_{KPOM}=S_{APC}-S_{AKM}=\frac{9S}{11}-\frac{9S}{26}=$$ $$=\frac{9S(26-11)}{26\cdot 11}=\frac{15\cdot 9S}{26\cdot 11}\to \frac{S_{AKM}}{S_{KPCM}}=\frac{9}{26}\cdot \frac{26\cdot 11}{15\cdot 9}=\frac{11}{15}.$$
Задание 1050
В треугольнике $$ABC$$ на его медиане $$BM$$ отмечена точка $$K$$ так, что $$BK:KM=7:3$$. Прямая $$AK$$ пересекает сторону $$BC$$ в точке $$P$$. Найдите отношение площади треугольника $$BKP$$ к площади треугольника $$KPCM$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 507
В треугольнике $$ABC$$ на его медиане $$BM$$ отмечена точка $$K$$ так, что $$BK:KM=6:7$$. Прямая $$AK$$ пересекает сторону $$BC$$ в точке $$P$$. Найдите отношение площади треугольника $$BKP$$ к площади треугольника $$ABK$$.