Задание 1972

Аналоги к этому заданию:

Задание 1972

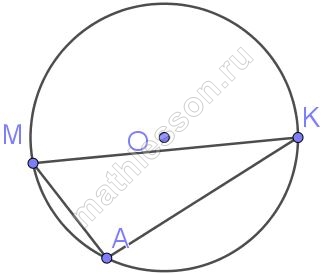
Вершины треугольника делят описанную около него окружность на три дуги, длины которых относятся как $$6:11:19$$. Найдите радиус окружности, если меньшая из сторон равна $$15$$.

Ответ: 15

Видео-решение Решение 1

ⓘ

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

1) Углы A,B,C - вписанные, потому равны половинам соответствующих дуг, потому отношение углов 6:11:29.

2) Т.к. $$\angle A+\angle B+\angle C=180^{\circ},$$ если $$\angle A=6x,$$ то: $$6x+11x+29x=180^{\circ}\to x=5\to \angle A=30^{\circ}.$$

3) Напротив меньшей стороны лежит меньший угол $$\to BC=15. R=\frac{a}{2\sin{\alpha}}=\frac{BC}{2\sin{A}}=\frac{15}{2\cdot \frac{1}{2}}=15$$

Аналоги к этому заданию:

Задание 4887

Вершины треугольника делят описанную около него окружность на три дуги, длины которых относятся как $$3:4:11$$. Найдите радиус окружности, если меньшая из сторон равна $$14$$.

Ответ: 14

Решение 1

ⓘ

Скрыть

Пусть меньший угол K, тогда по свойству треугольника меньшая сторона AM. Углы треугольника для окружности являются вписанными, следовательно, равны половинам дуг, на которые опираются, а значит и относятся так же , как и дуги.

Пусть угол К равен 3х, тогда M=4x и A=11x. По свойству углов треугольника: $$3x+4x+11x=180\Leftrightarrow$$$$x=10$$, тогда угол К составляет 30 градусов, а меньшая дуга MA составляет 60 градусов.

Угол MOA является центральным, следовательно $$\angle MOA=\smile MA=60^{\circ}$$, тогда треугольник MOA не только равнобедренный (OM=OA - радиусы), но и равносторонний, следовательно, MA=14

Задание 4486

Вершины треугольника делят описанную около него окружность на три дуги, длины которых относятся как $$1:2:3$$. Найдите радиус окружности, если меньшая из сторон равна $$15$$.

Ответ: 17

Видео-решение Решение 1

ⓘ

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

Если дуги, на которые опираются углы относятся как 1:2:3, то и углы относятся так же. Следовательно, добавим х к нашему отношению, получим, что углу равны x:2x:3x. Всего получаем x+2x+3x=6x. При этому сумма углов равна 180, значит 6x=180, x=30. Тогда мы имеем углы, равные 30,60,90. То есть у нас прямоугольный треугольник. Тогда меньшая сторона лежит на против меньшего угла в 30 градусов, а значит гипотенуза в два раза больше и равна 34. Радиус описанной окружности вокруг прямоугольного треугольника равен половине гипотенузы, то есть 34/2=17

Задание 1990

Вершины треугольника делят описанную около него окружность на три дуги, длины которых относятся как $$6:13:17$$. Найдите радиус окружности, если меньшая из сторон равна $$18$$.

Ответ: 18

Видео-решение Решение 1

ⓘ

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

Пусть дуги $$6x;13x;17x$$. Тогда $$6x+13x+17x=360\to x=10$$ т.е. дуги $$60^{\circ}; 130^{\circ}; 170^{\circ}$$. Пусть $$\angle C$$ опирается на дугу в $$60^{\circ}\to \angle C=30^{\circ}$$ (вписанный) $$\to AB=18, R=\frac{AB}{2\sin{C}}=\frac{18}{2\cdot \frac{1}{2}}=18$$