Задание 1722
Задание 1722
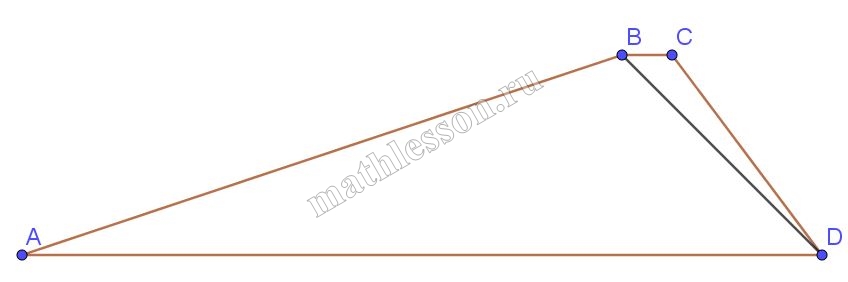
Основания $$BC$$ и $$AD$$ трапеции $$ABCD$$ равны соответственно $$4,5$$ и $$18$$, $$BD=9$$. Докажите, что треугольники $$CBD$$ и $$BDA$$ подобны.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Аналоги к этому заданию:
Задание 3192
Основания $$BC$$ и $$AD$$ трапеции $$ABCD$$ равны соответственно $$4$$ и $$64$$, $$BD=16$$. Докажите, что треугольники $$CBD$$ и $$BDA$$ подобны.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
1) $$\angle CBD=\angle BDA$$(накрест лежащие)
2) $$\frac{BD}{AD}=\frac{BC}{BD}$$. С учетом п.1 получим, что $$\Delta BCD\sim \Delta BDA$$
Задание 1989
Основания $$BC$$ и $$AD$$ трапеции $$ABCD$$ равны соответственно $$5$$ и $$45$$, $$BD=15$$. Докажите, что треугольники $$CBD$$ и $$BDA$$ подобны.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
1)$$\angle CBD=\angle BDA$$ (накрест лежащие при $$BC\parallel AD$$)
2) Рассмотрим $$\triangle BCD$$ и $$\triangle BDA$$ (в числителе сторона $$\triangle BCD$$, в знаменателе $$\triangle BDA$$): $$\frac{BC}{BD}=\frac{5}{15}=\frac{1}{3}; \frac{BD}{AD}=\frac{15}{45}=\frac{1}{3}\to \frac{BC}{BD}=\frac{BD}{AD}$$. С учетом 1 пункта: $$\triangle BCD\approx \triangle BDA$$
Задание 2515
Основания $$BC$$ и $$AD$$ трапеции $$ABCD$$ равны соответственно $$3$$ и $$12$$, $$BD=6$$. Докажите, что треугольники $$CBD$$ и $$BDA$$ подобны.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
