Задание 1988
Задание 1988
Зонты
Две подруги Оля и Аня задумались о том, как рассчитать площадь поверхности зонта.
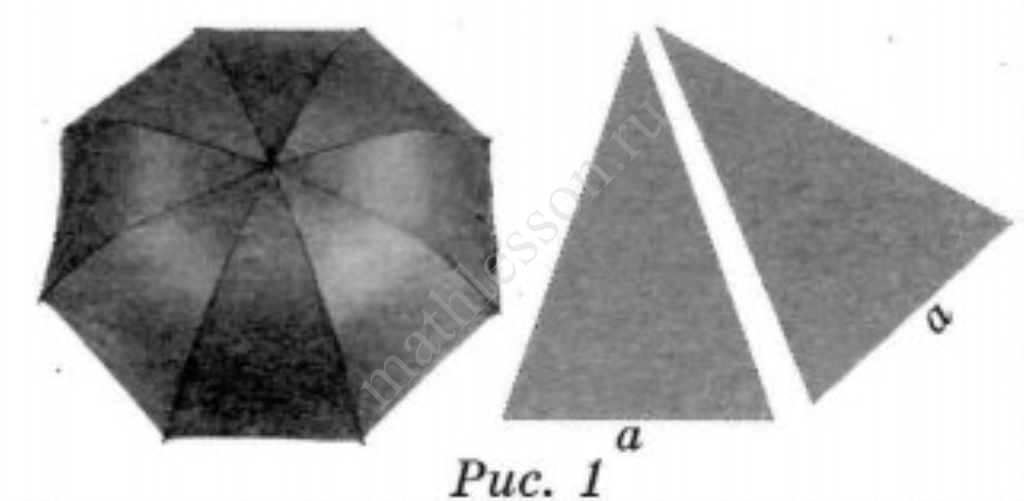
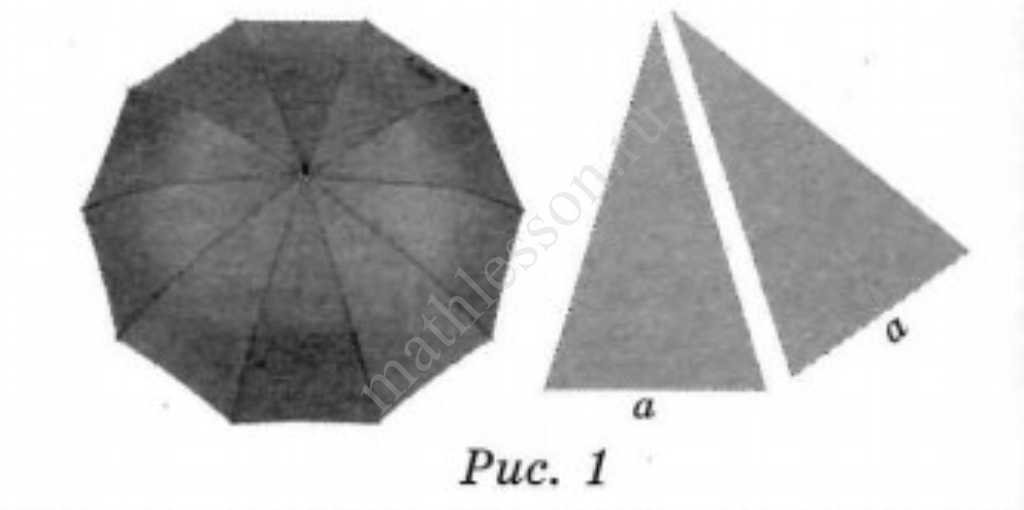
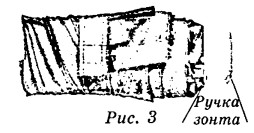
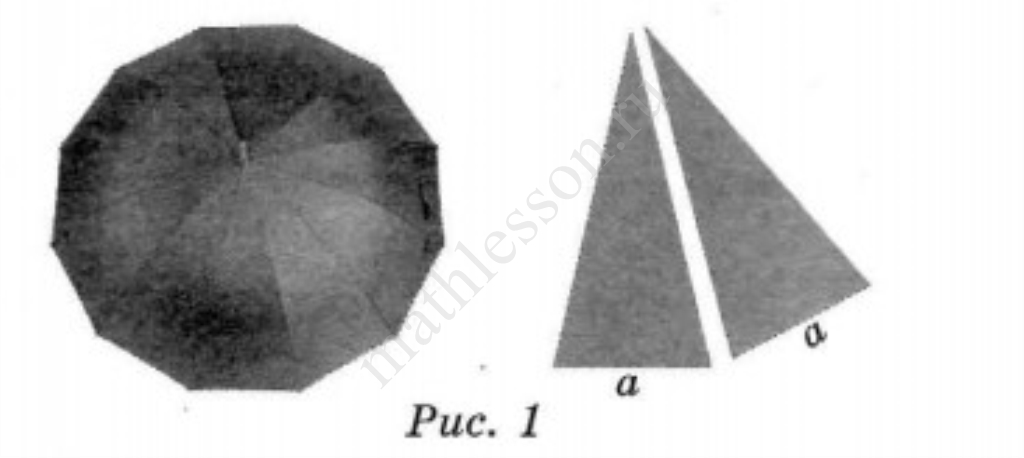
На первый взгляд зонт кажется круглым, а его купол напоминает часть сферы (сферический сегмент). Но если присмотреться, то видно, что купол зонта состоит из двенадцати отдельных клиньев, натянутых на каркас из двенадцати спиц (рис. 1). Сферическая форма в раскрытом состоянии достигается за счёт гибкости спиц и эластичности ткани, из которой изготовлен зонт.
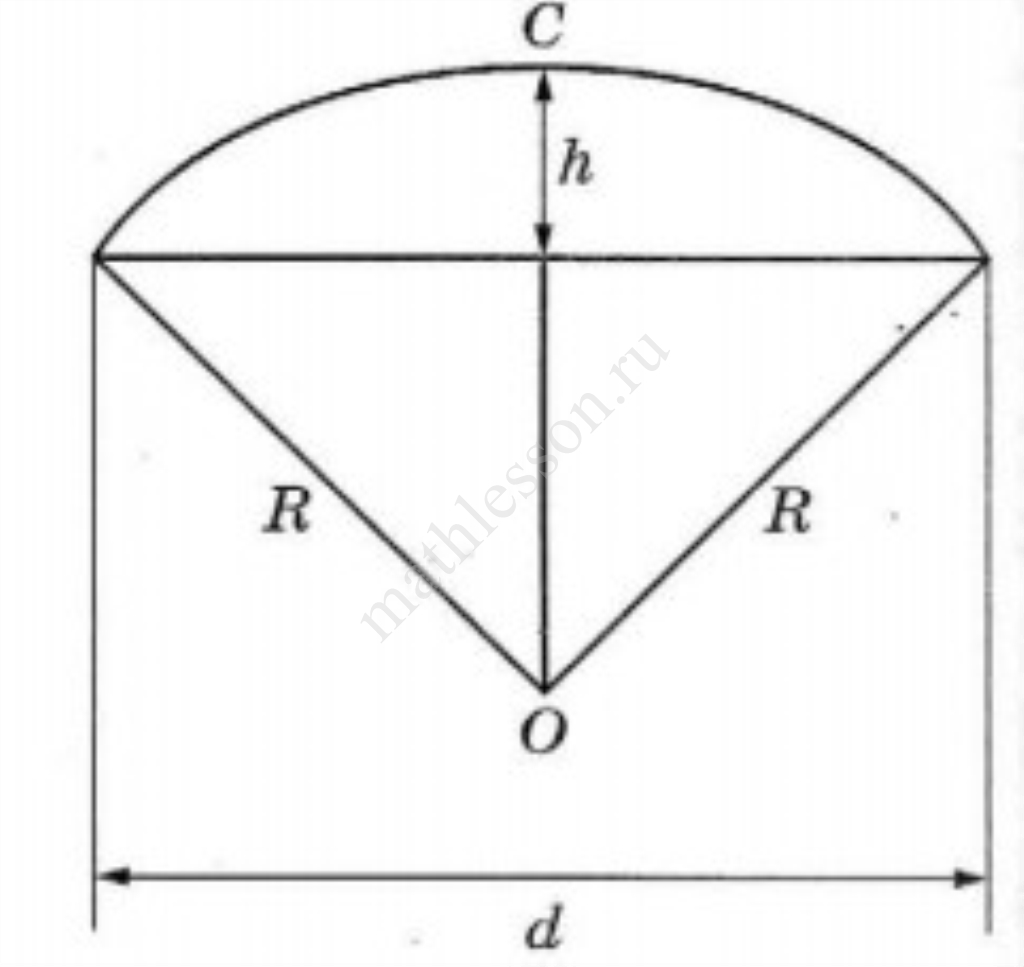
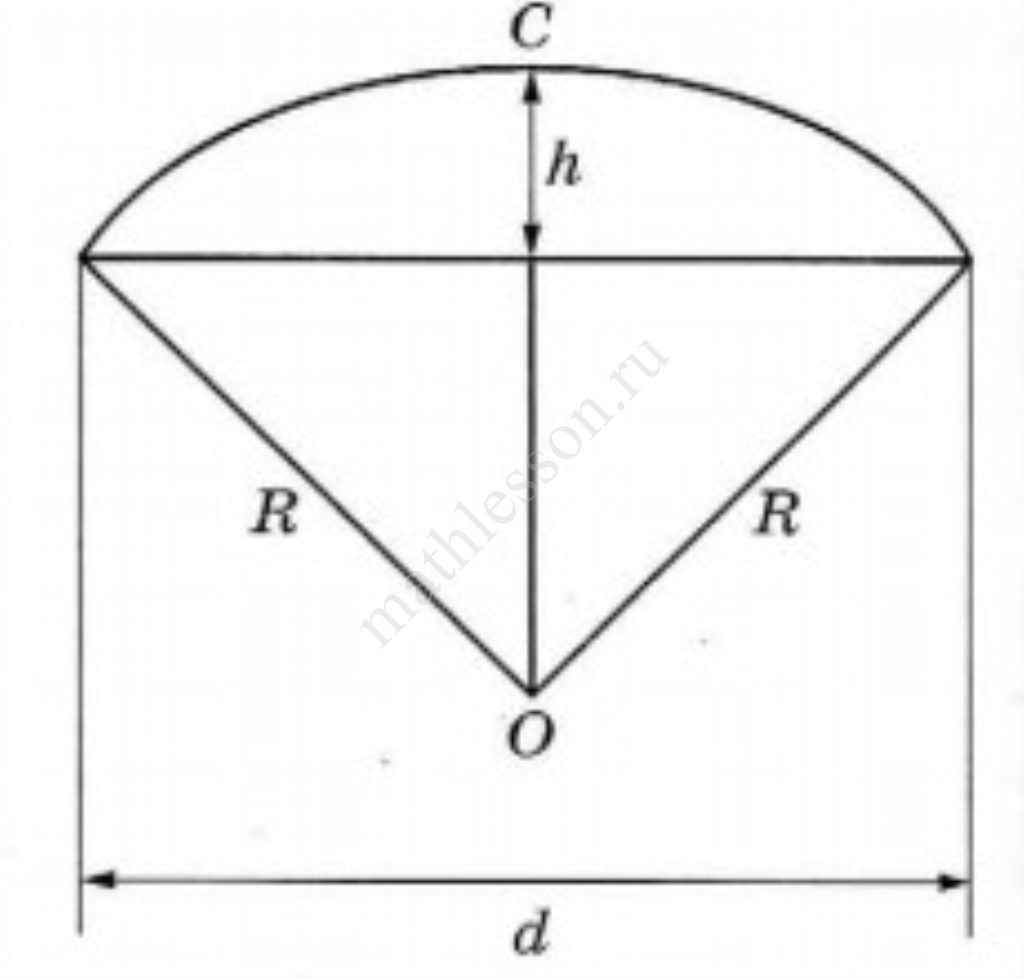
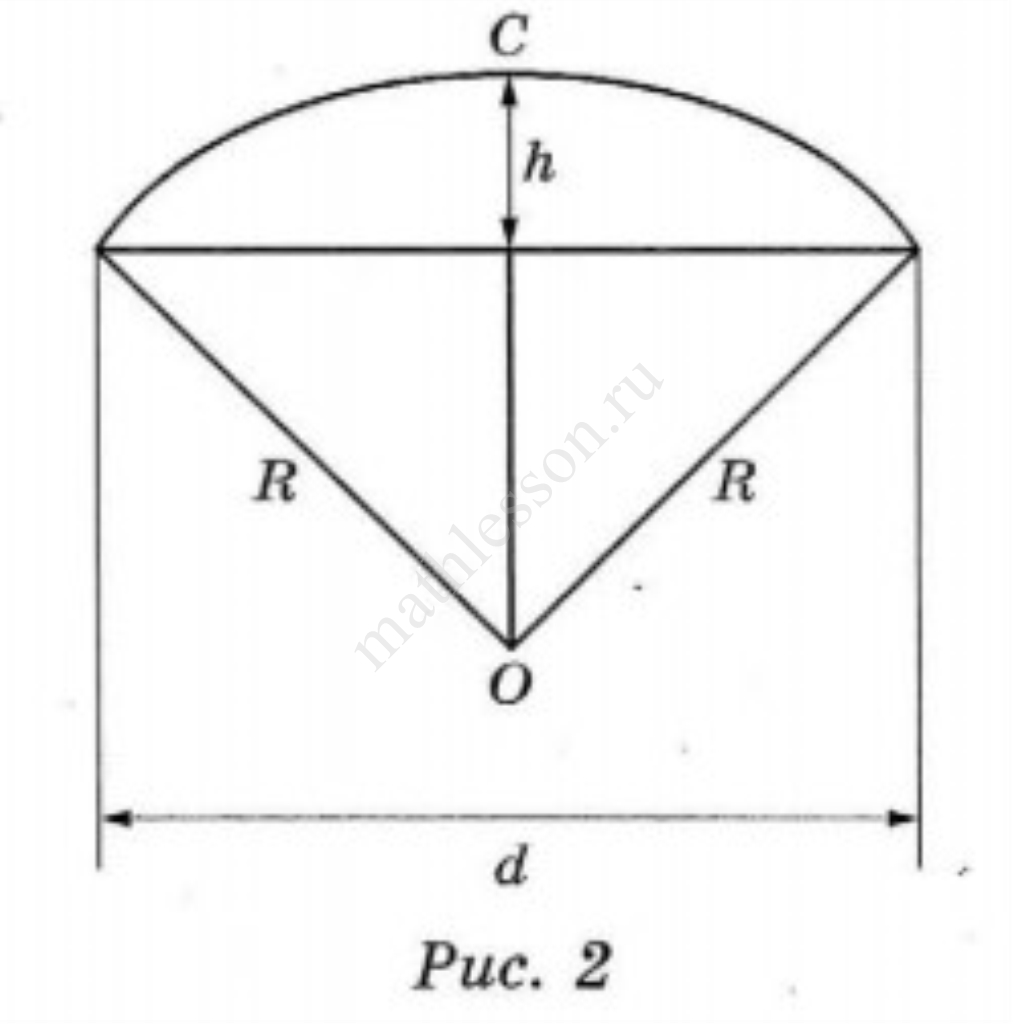
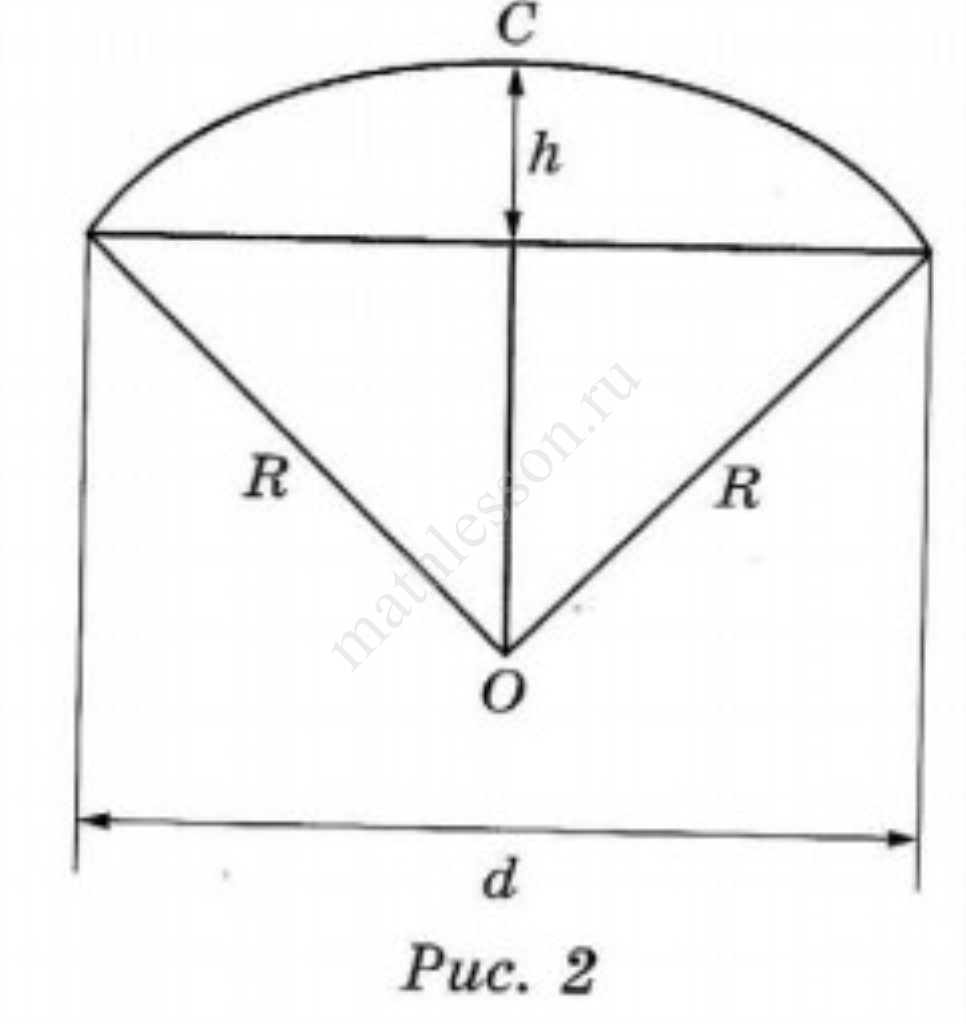
Оля и Аня сумели измерить расстояние между концами соседних спиц $$a$$. Оно оказалось равно $$28$$ см. Высота купола зонта $$h$$ (рис. 2) оказалась равна $$27$$ см, а расстояние $$d$$ между концами спин, образующих дугу окружности, проходящей через вершину зонта, — ровно $$108$$ см.
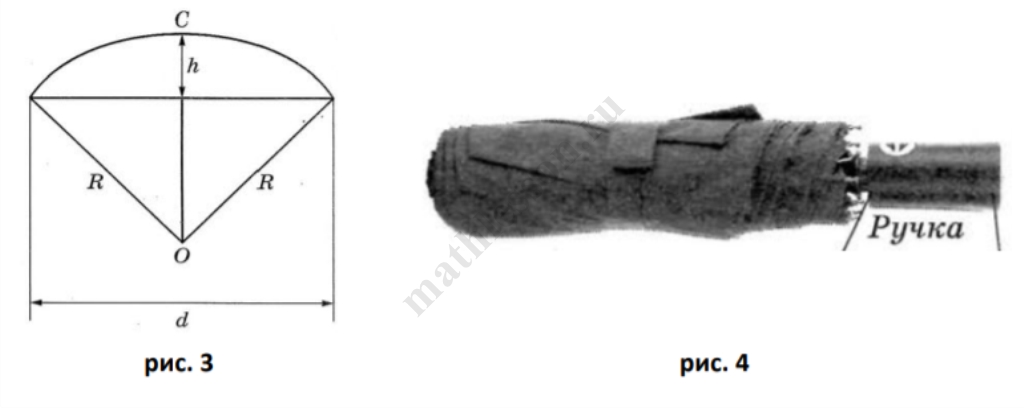
- Длина зонта в сложенном виде равна $$27$$ см и складывается из длины ручки (рис. 3) и трети длины спицы (зонт в три сложения). Найдите длину спицы, если длина ручки зонта равна $$6,8$$ см.
- Поскольку зонт сшит из треугольников, рассуждала Оля, площадь его поверхности можно найти как сумму площадей треугольников. Вычислите площадь поверхности зонта методом Оли, если высота каждого равнобедренного треугольника, проведённая к основанию, равна $$59$$ см. Ответ дайте в квадратных сантиметрах с округлением до десятков.
- Аня предположила, что купол зонта имеет форму сферического сегмента. Вычислите радиус $$R$$ сферы купола, зная, что $$OC = R$$ (рис. 2). Ответ дайте в сантиметрах.
- Аня нашла площадь купола зонта как площадь поверхности сферического сегмента по формуле $$S = 2\pi Rh$$, где R — радиус сферы, a h — высота сегмента. Рассчитайте площадь поверхности купола способом Ани. Число $$\pi$$ округлите до $$3,14$$. Ответ дайте в квадратных сантиметрах с округлением до целого.
- Рулон ткани имеет длину $$20$$ м и ширину $$90$$ см. На фабрике из этого рулона были вырезаны треугольные клинья для $$15$$ зонтов, таких же, как зонт, который был у Оли и Ани. Каждый треугольник с учётом припуска на швы имеет площадь $$850$$ кв. см. Оставшаяся ткань пошла в обрезки. Сколько процентов ткани рулона пошло в обрезки?
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


1) Длина $$\frac{1}{3}$$ спицы: $$27-6,8=20,2$$ см. Тогда длина всей спицы: $$3\cdot 20,2=60,6$$ см.
2) Площадь одного треугольника: $$S_1=\frac{1}{2}\cdot 28\cdot 59=826$$. Тогда площадь поверхности зонта: $$S_2=12\cdot 826=9912\approx 9910$$ см$$^2$$.
3) Пусть $$OM=x$$; из $$\triangle OLN: OM$$ - высота и медиана $$\to MN=\frac{d}{2}=54$$ см. Из $$\triangle OMN: OM^2+MN^2=ON^2\to x^2+54^2=(x+27)^2\leftrightarrow 54^2=54x+27^2\leftrightarrow$$ $$\leftrightarrow 54x=2916-729\to x=40,5\to R=40,5+27=67,5$$ см.
4) $$S=2\cdot 3,14\cdot 67,5\cdot 27=11445,3\approx 11445$$ см$$^2$$.
5) Количество клиньев: $$15\cdot 12=180$$ шт. Площадь клиньев: $$\frac{180\cdot 850}{100\cdot 100}=15,3$$ м$$^2$$. Площадь рулона: $$20\cdot 0,9=18$$ м$$^2$$. Обрезков: $$18-15,3=2,7$$ м$$^2$$. В процентах $$\frac{2,7}{18}\cdot 100=15%$$
Задание 1733
Зонты
Две подруги Ира и Юля задумались о том, как рассчитать площадь поверхности зонта.
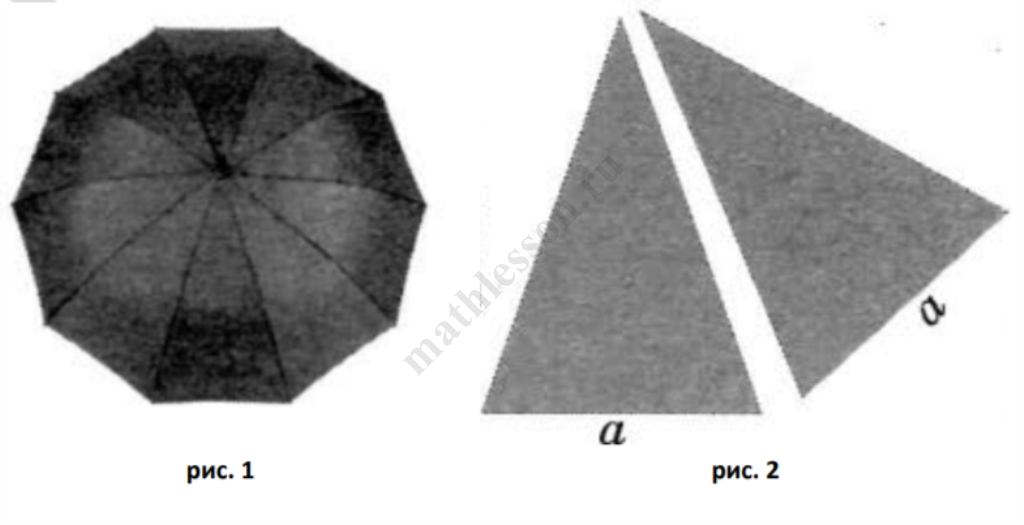
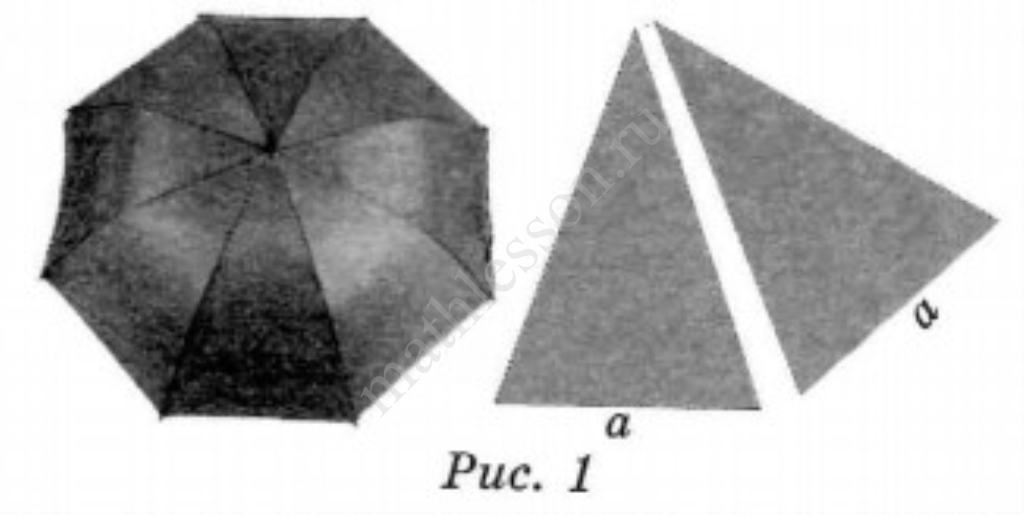
На первый взгляд зонт кажется круглым, а его купол напоминает часть сферы (сферический сегмент). Но если присмотреться, то видно, что купол зонта состоит из восьми отдельных клиньев, натянутых на каркас из восьми спиц (рис. 1). Сферическая форма в раскрытом состоянии достигается за счёт гибкости спиц и эластичности ткани, из которой изготовлен зонт.
Ира и Юля сумели измерить расстояние между концами соседних спиц $$a$$. Оно оказалось равно $$40$$ см. Высота купола зонта $$h$$ (рис. 2) оказалась равна $$26$$ см, а расстояние $$d$$ между концами спиц, образующих дугу окружности, проходящей через вершину зонта, — ровно $$104$$ см.
1) Длина зонта в сложенном виде равна $$26$$ см и складывается из длины ручки (рис. 3) и трети длины спицы (зонт в три сложения). Найдите длину спицы, если длина ручки зонта равна $$6,5$$ см.
2) Поскольку зонт сшит из треугольников, рассуждала Ира, площадь его поверхности можно найти как сумму площадей треугольников. Вычислите площадь поверхности зонта методом Иры, если высота каждого равнобедренного треугольника, проведённая к основанию, равна $$55$$ см. Ответ дайте в квадратных сантиметрах.
3) Юля предположила, что купол зонта имеет форму сферического сегмента. Вычислите радиус $$R$$ сферы купола, зная, что $$OC = R$$ (рис. 2). Ответ дайте в сантиметрах.
4) Юля нашла площадь купола зонта как площадь поверхности сферического сегмента по формуле $$S=2\pi Rh$$, где $$R$$ — радиус сферы, а $$h$$ — высота сегмента. Рассчитайте площадь поверхности купола способом Юли. Число л округлите до $$3,14$$. Ответ дайте в квадратных сантиметрах с округлением до целого.
5) Рулон ткани имеет длину $$30$$ м и ширину $$90$$ см. На фабрике из этого рулона были вырезаны треугольные клинья для $$27$$ зонтов, таких же, как зонт, который был у Иры и Юли. Каждый треугольник с учётом припуска на швы имеет площадь $$1150$$ кв. см. Оставшаяся ткань пошла в обрезки. Сколько процентов ткани рулона пошло в обрезки?
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 1743
Зонты
Два друга Коля и Боря задумались о том, как рассчитать площадь поверхности зонта.
На первый взгляд зонт кажется круглым, напоминает часть сферы сегмент). Но если то видно, что купол зонта отдельных клиньев, состоянии а его купол (сферический присмотреться, состоит из десяти натянутых на каркас из десяти спиц (рис. 1). Сферическая форма в раскрытом достигается за счёт гибкости спиц и эластичности ткани, из которой изготовлен зонт.
Коля и Боря сумели измерить расстояние между концами соседних спиц $$a$$. Оно оказалось равно $$36$$ см. Высота купола зонта $$h$$ (рис. 2) оказалась равна $$20$$ см, а расстояние $$d$$ между концами спиц, образующих дугу окружности, проходящей через вершину зонта, ровно $$116$$ см.
1) Длина зонта в сложенном виде равна $$27$$ см и складывается из длины ручки (рис. 3) и трети длины спицы (зонт в три сложения). Найдите длину спицы, если длина ручки зонта равна $$6,5$$ см.
2) Поскольку зонт сшит из треугольников, рассуждал Коля, площадь его поверхности можно найти как сумму площадей треугольников. Вычислите площадь поверхности зонта методом Коли, если высота каждого равнобедренного треугольника, проведённая к основанию, равна $$58,8$$ см. Ответ дайте в квадратных сантиметрах с округлением до десятков.
3) Боря предположил, что купол зонта имеет форму сферического сегмента. Вычислите радиус $$R$$ сферы купола, зная, что $$OC=R$$ (рис. 2). Ответ дайте в сантиметрах.
4) Боря нашёл площадь купола зонта как площадь поверхности сферического сегмента по формуле $$S=2\pi Rh$$, где $$R — радиус сферы, а $$h$$ — высота сегмента. Рассчитайте площадь поверхности купола способом Бори. Число $$\pi$$ округлите до $$3,14$$. Ответ дайте в квадратных сантиметрах с округлением до целого.
5) Рулон ткани имеет длину $$25$$ м и ширину $$80$$ см. На фабрике из этого рулона были вырезаны треугольные клинья для $$16$$ зонтов, таких же, как зонт, который был у Коли и Бори. Каждый треугольник с учётом припуска на швы имеет площадь $$1100$$ кв. см. Оставшаяся ткань пошла в обрезки. Сколько процентов ткани рулона пошло в обрезки?
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 2007
Зонты
Два друга Петя и Вася задумались о том, как рассчитать площадь поверхности зонта. На первый взгляд зонт кажется круглым, а его купол напоминает часть сферы (сферический сегмент). Но если присмотреться, то видно, что купол зонта состоит из восьми отдельных клиньев, натянутых на каркас из восьми спиц (рис. 1). Сферическая форма в раскрытом состоянии достигается за счёт гибкости спиц и эластичности ткани, из которой изготовлен зонт. Петя и Вася сумели измерить расстояние между концами соседних спиц $$a$$. Оно оказалось равно $$38$$ см. Высота купола зонта $$h$$ (рис. 2) оказалась равна $$25$$ см, а расстояние $$d$$ между концами спиц, образующих дугу окружности, проходящей через вершину зонта, — ровно $$100$$ см.
1. Длина зонта в сложенном виде равна $$25$$ см и складывается из длины ручки (рис. 3) и трети длины спицы (зонт в три сложения). Найдите длину спицы, если длина ручки зонта равна $$6,2$$ см.
2. Поскольку зонт сшит из треугольников, рассуждал Петя, площадь его поверхности можно найти как сумму площадей треугольников. Вычислите площадь поверхности зонта методом Пети, если высота каждого равнобедренного треугольника, проведённая к основанию, равна $$53,1$$ см. Ответ дайте в квадратных сантиметрах с округлением до десятков.
3. Вася предположил, что купол зонта имеет форму сферического сегмента. Вычислите радиус $$R$$ сферы купола, зная, что $$OC = R$$ (рис. 2). Ответ дайте в сантиметрах.
4. Вася нашёл площадь купола зонта как площадь поверхности сферического сегмента по формуле $$S = 2\pi Rh$$, где $$R$$ — радиус сферы, a $$h$$ — высота сегмента. Рассчитайте площадь поверхности купола способом Васи. Число $$\pi$$ округлите до $$3,14$$. Ответ дайте в квадратных сантиметрах с округлением до целого.
5. Рулон ткани имеет длину $$35$$ м и ширину $$80$$ см. На фабрике из этого рулона были вырезаны треугольные клинья для $$29$$ зонтов, таких же, как зонт, который был у Пети и Васи. Каждый треугольник с учётом припуска на швы имеет площадь $$1050$$ кв. см. Оставшаяся ткань пошла в обрезки. Сколько процентов ткани рулона пошло в обрезки?
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
1) Длина $$\frac{1}{3}$$ спицы: $$25-6,2=18,8$$ см. Тогда длина всей спины: $$3*18,8=56,4$$ см
2) Площадь одного треугольника $$S_1=\frac{1}{2} \cdot 38 \cdot 53,1=1008,9$$ см$$^{2}$$. Тогда площадь поверхности зонта: $$S_2=1008,9\cdot 8=8071,2$$ см$$^{2}$$.
3) Пусть x - высота равнобедреннего треугольника OMN. Тогда $$HN=50; ON=25+x.$$ По теореме Пифагора: $$x^{2}+2500=x^{2}+50x+625\to x=37,5\to R=37,5+25=62,5$$ см.
4) $$S=2\cdot 3,14\cdot 62,5\cdot 25=9812,5$$ см$$^{2}$$ $$\approx 9813$$ см$$^{2}$$.
5) Ушло на треугольники: $$29\cdot 8=1050=243600$$ см$$^{2}$$ $$=\frac{243600}{100\cdot 100}$$ м$$^{2}$$ $$=24,36$$ м$$^{2}$$. Площадь рулона: $$35\cdot 0,8=28$$ м$$^{2}$$ В обрезки пошло: $$\frac{28-24,36}{28}=100=13%$$
Задание 1370
Зонты
Два друга, Коля и Боря, задумались о том, как рассчитать площадь поверхности зонта. На первый взгляд зонт кажется круглым, а его купол напоминает часть сферы (сферический сегмент). Но если присмотреться, то видно, что купол зонта состоит из десяти отдельных клиньев, натянутых на каркас из десяти спиц (см. выше рис. 1). Сферическая форма в раскрытом состоянии достигается за счёт гибкости спиц и эластичности ткани, из которой изготовлен зонт.
Коля и Боря сумели измерить расстояние между концами соседних спиц $$a$$(см. выше рис. 2). Оно оказалось равно $$36$$ см. Высота купола зонта $$h$$(см. выше рис. 3) оказалась равна $$20$$ см, а расстояние $$d$$ между концами спиц, образующих дугу окружности, проходящей через вершину зонта, – $$116$$ см.
1. Длина зонта в сложенном виде равна $$27$$ см. Она складывается из длины ручки (см. выше рис. 4) и трети длины спицы (зонт в три сложения). Найдите длину спицы (в см), если длина ручки зонта равна $$6,5$$ см.
2. Поскольку зонт сшит из треугольников, рассуждал Коля, площадь его поверхности можно найти как сумму площадей треугольников. Вычислите площадь поверхности (в см 2) зонта методом Коли, если высота каждого равнобедренного треугольника, проведённая к основанию, равна $$58,8$$ см. Ответ округлите до десятков.
3. Боря предположил, что купол зонта имеет форму сферического сегмента. Вычислите радиус $$R$$ сферы купола (в см), зная, что $$OC=R$$(см. выше рис. 3).
4. Боря нашёл площадь купола зонта как площадь поверхности сферического сегмента по формуле $$S=2\pi Rh$$, где $$R$$ – радиус сферы, $$h$$ – высота сегмента. Рассчитайте площадь поверхности купола зонта (в см2) методом Бори. Число $$\pi$$ округлите до $$3,14$$. Ответ округлите до целого числа.
5. Рулон ткани имеет длину $$25$$ м и ширину $$80$$ см. На фабрике из этого рулона были вырезаны треугольные клинья для 16 зонтов, таких же, как зонт, который был у Коли и Бори. Каждый треугольник, с учётом пропуска на швы, имеет площадь $$1 110$$ см2. Оставшаяся ткань пошла на обрезки. Сколько процентов ткани рулона пошло на обрезки?
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 1549
Зонты
Два друга Дима и Юра задумались о том, как рассчитать площадь поверхности зонта.
На первый взгляд зонт кажется круглым, а его купол напоминает часть сферы (сферический сегмент). Но если присмотреться, то видно, что купол зонта состоит из двенадцати отдельных клиньев, натянутых на каркас из двенадцати спиц (рис. 1). Сферическая форма в раскрытом состоянии достигается за счёт гибкости спиц и эластичности ткани, из которой изготовлен зонт.
Дима и Юра сумели измерить расстояние между концами соседних спиц $$a$$. Оно оказалось равно $$30$$ см. Высота купола зонта $$h$$ (рис. 2) оказалась равна $$29$$ см, а расстояние $$d$$ между концами спиц, образующих дугу окружности, проходящей через вершину зонта, - ровно $$116$$ см.
1. Длина зонта в сложенном виде равна $$28$$ см и складывается из длины ручки (рис. 3) и трети длины спицы (зонт в три сложения). Найдите длину спицы, если длина ручки зонта равна $$6,2$$ см.
2. Поскольку зонт сшит из треугольников, рассуждал Дима, площадь его поверхности можно найти как сумму площадей треугольников. Вычислите площадь поверхности зонта методом Димы, если высота каждого равнобедренного треугольника, проведённая к основанию, равна $$63,7$$ см. Ответ дайте в квадратных сантиметрах с округлением до десятков.
3. Юра предположил, что купол зонта имеет форму сферического сегмента. Вычислите радиус $$R$$ сферы купола, зная, что $$OC=R$$ (рис. 2). Ответ дайте в сантиметрах.
4. Юра нашёл площадь купола зонта как площадь поверхности сферического сегмента по формуле $$S=2\pi Rh$$, где $$R$$ - радиус сферы, a $$h$$ - высота сегмента. Рассчитайте площадь поверхности купола способом Юры. Число $$\pi$$ округлите до $$3,14$$. Ответ дайте в квадратных сантиметрах с округлением до целого.
5. Рулон ткани имеет длину $$16$$ м и ширину $$150$$ см. На фабрике из этого рулона были вырезаны треугольные клинья для $$18$$ зонтов, таких же, как зонт, который был у Димы и Юры. Каждый треугольник с учётом припуска на швы имеет площадь $$1000$$ кв. см. Оставшаяся ткань пошла в обрезки. Сколько процентов ткани рулона пошло в обрезки?
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 438
Зонты
Два друга Юра и Ваня задумались о том, как рассчитать площадь поверхности зонта.
На первый взгляд зонт кажется круглым, а его купол напоминает часть сферы (сферический сегмент). Но если присмотреться, то видно, что купол зонта состоит из десяти отдельных клиньев, натянутых на каркас из десяти спиц (рис. 1). Сферическая форма в раскрытом состоянии достигается за счёт гибкости и эластичности ткани, из которой изготовлен зонт Юра и Ваня сумели измерить расстояние между концами соседних спиц $$a$$. Оно оказалось равно $$34$$ см. Высота купола зонта $$h$$ (рис. 2) оказалась равна $$25$$ см, расстояние $$d$$ между концами спиц, образуют дугу зонта, окружности, проходящей через — ровно $$110$$ см.
1. Длина зонта в сложенном виде равна $$26,5$$ см и складывается из длины ручки (рис. 3) и трети длины спицы (зонт в три сложения). Найдите длину спицы, если длина ручки зонта равна $$6,3$$ см.
2. Поскольку зонт сшит из треугольников, рассуждал Юра, площадь его поверхности можно найти как сумму площадей треугольников. Вычислите площадь поверхности зонта методом Юры, если высота каждого равнобедренного треугольника, проведённая к основанию, равна $$58,2$$ см. Ответ дайте в квадратных сантиметрах с округлением до десятков.
3. Ваня предположил, что купол зонта имеет форму сферического сегмента. Вычислите радиус $$R$$ сферы купола, зная, что $$OC=R$$ (рис. 2). Ответ дайте в сантиметрах.
4. Ваня нашёл площадь купола зонта как площадь поверхности сферического сегмента по формуле $$S=2πRh$$, где $$R$$ — радиус сферы, а $$h$$ — высота сегмента. Рассчитайте площадь поверхности купола способом Вани. Число $$π$$ округлите до $$3,14$$. Ответ дайте в квадратных сантиметрах с округлением до целого.
5. Рулон ткани имеет длину $$20$$ м и ширину $$150$$ см. На фабрике из этого рулона были вырезаны треугольные клинья для $$26$$ зонтов, таких же, как зонт, который был у Юры и Вани. Каждый треугольник с учётом припуска на швы имеет площадь $$1050$$ кв. см. Оставшаяся ткань пошла в обрезки. Сколько процентов ткани рулона пошло в обрезки?


.jpg)
.jpg)