Параболы
Задание 1192
Постройте график функции $$y = -4 - \frac{x^4 + x^3}{x^2 + x}$$ и определите, при каких значениях $$m$$ прямая $$y = m$$ имеет с графиком ровно две общие точки.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 1552
Постройте график функции $$y = \frac{(0{,}25x^2 + 0{,}5x) \cdot |x|}{x + 2}$$ и определите, при каких значениях $$m$$ прямая $$y = m$$ не имеет с графиком ни одной общей точки.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 1170
Постройте график функции $$y = \frac{(x + 3)(x^2 - 3x + 2)}{x - 2}$$ и определите, при каких значениях $$m$$ прямая $$y = m$$ имеет с графиком ровно одну общую точку.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 2039
Постройте график функции $$y = \frac{(x^2 - 4x + 3)(x^2 - x - 2)}{x^2 - 2x - 3}$$ и определите, при каких значениях $$m$$ прямая $$y = m$$ имеет с графиком ровно одну общую точку.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Учтем область определения функции D(x): $$x^{2}-2x-3\neq 0\Leftrightarrow$$$$x\neq -1;3$$
Разложим числитель на множители:
Тогда с учетом D(x): $$y=\frac{(x^{2}-4x+3)(x^{2}-x-2)}{x^{2}-2x-3}=$$$$\frac{(x-3)(x-1)(x-2)(x+1)}{(x+1)(x-3)}=$$$$(x-1)(x-2)$$
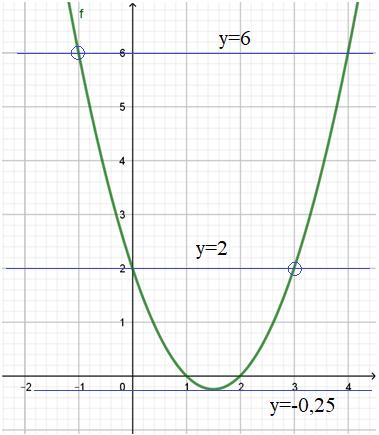
Построим график функции:
Прямая y=m - параллельна оси оХ. Будет иметь одну точку пересечения в следующих случаях: -0,25;2;6
Задание 3864
Постройте график функции $$y = \frac{(x^2 + 6{,}25)(x - 1)}{1 - x}$$ и определите, при каких значениях $$k$$ прямая $$y = kx$$ имеет с графиком ровно одну общую точку.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 2557
Постройте график функции $$y = \frac{x^4 - 13x^2 + 36}{(x - 3)(x + 2)}$$. Найдите все значения $$m$$, при каждом из которых прямая $$y = m$$ имеет с графиком функции ровно одну общую точку.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 3885
Постройте график функции $$y = \left\{ \begin{aligned} 2x - x^2,&\ x \ge 0 \\ -4x - x^2,&\ x < 0 \end{aligned} \right.$$ и определите, при каких значениях $$m$$ прямая $$y = m$$ имеет с графиком ровно три общие точки.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


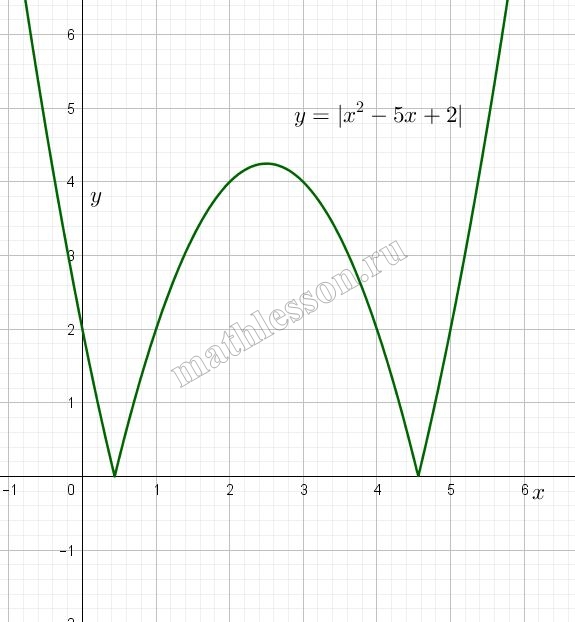
Задание 3839
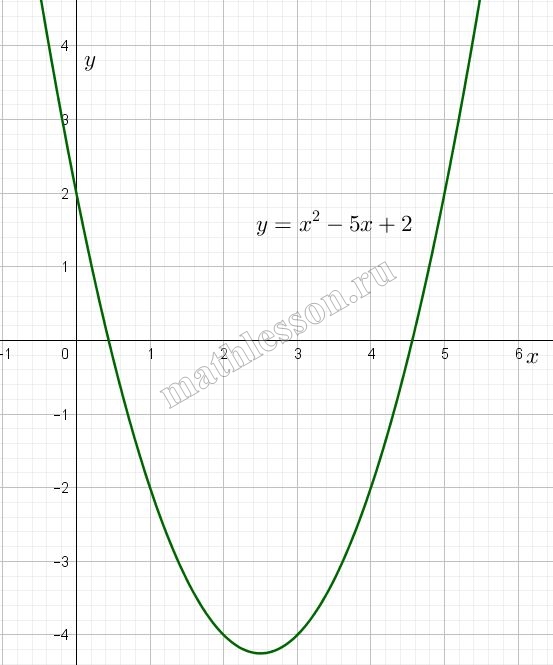
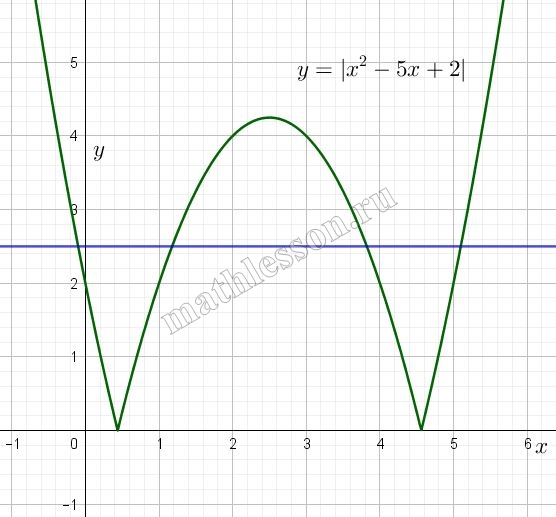
Постройте график функции $$y = |x^2 - 5x + 2|$$. Какое наибольшее число общих точек график данной функции может иметь с прямой, параллельной оси абсцисс?
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 3051
Постройте график функции $$y = |x^2 - 6|x| + 4| - 2$$ и определите, при каких значениях $$m$$ прямая $$y = m$$ имеет с графиком наибольшее число общих точек.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Расскроем первый модуль:
1) При $$x\geq 0$$ : $$y=\left | x^{2}-6x+4 \right |-2$$
Рассмотрим подмодульное выражение: $$x^{2}-6x+4=0$$: $$D=36-16=20\Rightarrow$$ $$x_{1}, x_{2}=\frac{6 \pm \sqrt{20}}{2}=3 \pm \sqrt{5}$$
- тогда при $$x \in [0;3-\sqrt{5}]\cup [3+\sqrt{5}; +\infty )$$: $$y=x^{2}-6x+4-2=x^{2}-6x+2(1)$$
- при $$x \in (3-\sqrt{5}; 3+\sqrt{5})$$: $$y=-x^{2}+6x-6(2)$$
2) При $$x<0$$ имеем $$y=\left | x^{2}+6x+4\right |-2$$
Рассмотрим подмодульное выражение : $$x^{2}+6x+4=0\Leftrightarrow$$ $$x_{1,2}=-3\pm \sqrt{5}$$
- тогда при $$x \in (-\infty ; -3-\sqrt{5}]\cup [-3+\sqrt{5};0)$$ имеем: $$y=x^{2}+6x+4+2=x^{2}+6x-2(3)$$
- при $$x \in (-3-\sqrt{5}; -3+\sqrt{5}):$$ $$y=-x^{2}-6x-6(4)$$
Построим график функции
Видим, что наибольшее количество пересечений (8) будет при $$m \in (-2;2)$$
Задание 2593
Постройте график функции $$y = |x| (x - 1) - 3x$$. Найдите все значения $$m$$, при каждом из которых прямая $$y = m$$ имеет с графиком функции ровно две общие точки.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Раскроме модуль: $$y=\left\{\begin{matrix}x(x-1)-3x=x^{2}-4x,x\geq0(1)&\\-x(x-1)-3x=-x^{2}-2x,x<0(2)&\end{matrix}\right.$$
В обоих случаях части парабол, ограниченные осью Oy (слева и справа сосответственно)
Найдем вершины:
1) $$x_{0}=-\frac{-4}{2}=2$$ $$\Rightarrow$$ $$y_{0}=2^{2}-4\cdot2=-4$$
2) $$x_{0}=-\frac{-2}{-2}=-1$$ $$\Rightarrow$$ $$y_{0}=-(-1)^{2}-2\cdot(-1)=1$$
Построим график
$$m\in{-4;1}$$
Задание 4005
Постройте график функции $$y = 2x|x| + x^2 - 6x$$ и определите, при каких значениях $$m$$ прямая $$y = m$$ имеет с графиком более двух общих точек.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!