Задание 235
Аналоги к этому заданию:
Задание 3769
Постройте график функции $$y = |x^2 + 6x + 5|$$ и определите, при каких значениях $$a$$ прямая $$y = a$$ имеет с графиком три общие точки.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
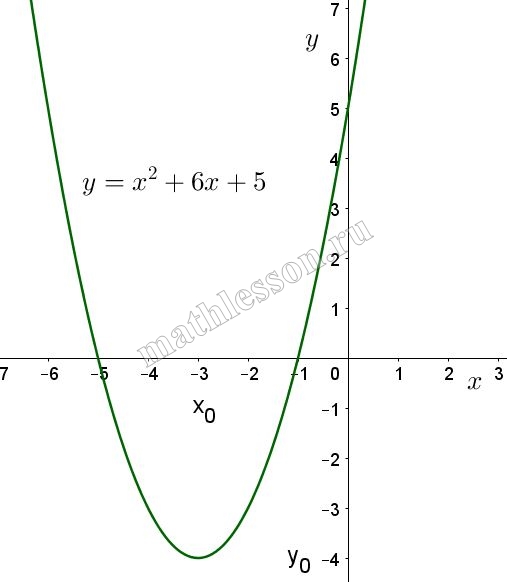
Рассмотрим график функции $$y_{1}=x^{2}+6x+5$$. Искомый будет отличаться от данного тем, что та часть параболы, которая находится под осью Ох симметрично отобразиться относительно оси Ох (в силу того, что модуль все отрицательные значения сделает положительными). Найдем вершину параболы: $$x_{0}=-\frac{b}{2a}=-\frac{6}{2}=-3$$ , $$y_{1}(3)=(-3)^{2}+6*(-3)+5=-4$$. Найдем еще несколько значений для функции $$y_{1}$$: $$y_{1}(-2)=-3 ; y_{1}(-1)=0 ; y_{1}(0)=5$$.
График квадратичной функции симметричен относительно оси $$x=x_{0}$$, в нашем случае относительно $$x=-3$$. Начертим график функции $$y_{1}$$:
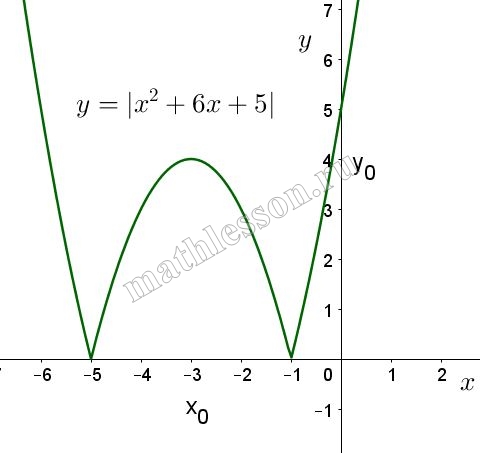
Отобразим симметрично относительно оси Ох ту часть параболы, которая располагается под осью Ох и получим график функции $$y=|x^{2}+6x+5|$$:
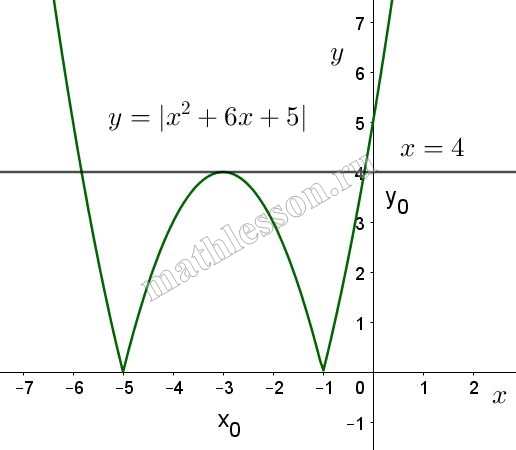
Очевидно, что прямая параллельная оси Оу будет иметь три точки пересечения с графиком данной функции при $$a=4$$:
Задание 4416
Постройте график функции $$y = |x^2 - 2x - 3|$$ и определите, при каких значениях $$a$$ прямая $$y = a$$ имеет с графиком три общие точки.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Текстовое решение временно отсутствует. Вы можете найти разбор в видео перед вариантом
Задание 3361
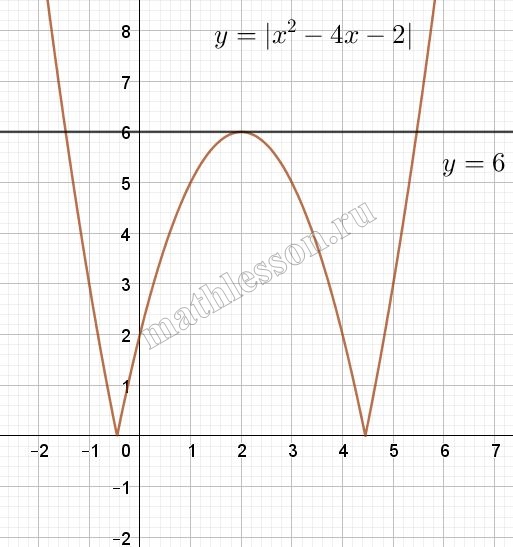
Постройте график функции $$y = |x^2 - 4x - 2|$$ и определите, при каких значениях $$c$$ прямая $$y = c$$ имеет с графиком три общие точки.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Данный график есть парабола $$y=x^{2}-4x-2$$, у которой часть ,которая располагается по Ox отображается симметрично Ox.
Найдем вершину параболы: $$x_{0}=-\frac{-4}{2}=2$$ $$y_{0}=\left | 4-8-2 \right |=6$$
$$y=c$$ - параллельна Ox, тогда при точки при y=6 , то есть c=6