Задание 2479
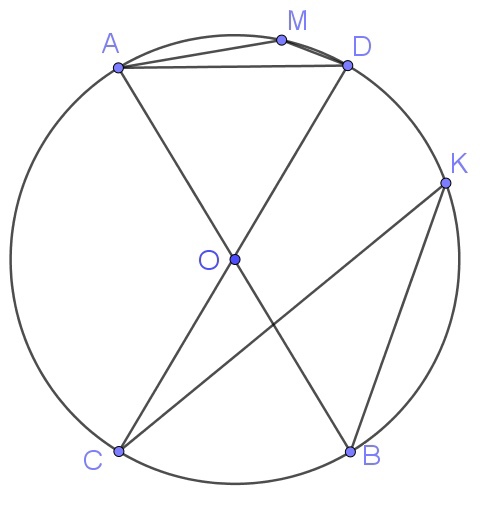
В окружности с центром $$O$$ отрезки $$AC$$ и $$BD$$ — диаметры. Угол $$AOD$$ равен $$108^\circ$$. Найдите угол $$ACB$$. Ответ дайте в градусах.
Так как АС и BD — диаметры, то дуги AD=BC и AB=CD. Найдем градусную меру дуги AB, на которую опирается вписанный угол ACB. Так как угол AOD = 108°, то градусная мера дуги AD = 108° и тогда градусная мера:
$$AB=\frac{360^{\circ}-AD-BC}{2}=$$$$\frac{360^{\circ}-2\cdot 108^{\circ}}{2}=72^{\circ}$$
Так как угол ACB является вписанным, то он равен половине градусной меры дуги, на которую опирается, то есть:
$$\angle ACB=\frac{AB}{2}=\frac{72^{\circ}}{2}=36^{\circ}$$
Задание 3272
На окружности по разные стороны от диаметра $$AB$$ взяты точки $$M$$ и $$N$$. Известно, что $$\angle NBA = 48^\circ$$. Найдите угол $$NMB$$. Ответ дайте в градусах.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
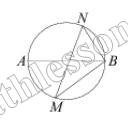
$$\smile AB=180=\smile AN+\smile NB$$
$$\smile AN=2\angle NBA=96$$
$$\smile NB=180-96=84$$
$$\angle NMB=\frac{\smile NB}{2}=\frac{84}{2}=42$$