Задание 3272
Задание 3272
На окружности по разные стороны от диаметра $$AB$$ взяты точки $$M$$ и $$N$$. Известно, что $$\angle NBA = 48^\circ$$. Найдите угол $$NMB$$. Ответ дайте в градусах.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
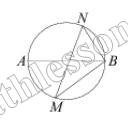
$$\smile AB=180=\smile AN+\smile NB$$
$$\smile AN=2\angle NBA=96$$
$$\smile NB=180-96=84$$
$$\angle NMB=\frac{\smile NB}{2}=\frac{84}{2}=42$$
Аналоги к этому заданию:
Задание 4012
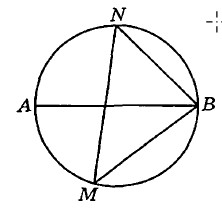
На окружности по разные стороны от диаметра $$AB$$ взяты точки $$M$$ и $$N$$. Известно, что $$\angle NBA = 38^\circ$$. Найдите угол $$NMB$$. Ответ дайте в градусах.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
$$\smile NA=38^{\circ}\cdot2=76^{\circ}$$; $$\smile NB=180^{\circ}-76^{\circ}=104^{\circ}$$; $$\angle NMB=\frac{104^{\circ}}{2}=52^{\circ}$$
Задание 4295
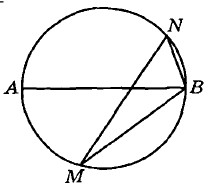
На окружности по разные стороны от диаметра $$AB$$ взяты точки $$M$$ и $$N$$. Известно, что $$\angle NBA = 36^\circ$$. Найдите угол $$NMB$$. Ответ дайте в градусах.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
∠NBA=36° - вписанный, значит дуга, на которую он опирается (AN) в два раза больше, то есть 72° Тогда дуга NB = 180° - 72°=108° (180°-AN так как AB - диаметр) ∠NMB=108°/2 = 54° (так как вписанный, значит равен половине градусной меры дуги, на которую опирается, то есть дуги NB
Задание 4468
На окружности по разные стороны от диаметра $$AB$$ взяты точки $$M$$ и $$N$$. Известно, что $$\angle NBA = 32^\circ$$. Найдите угол $$NMB$$. Ответ дайте в градусах.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Дуга NA в два раза больше вписанного угла, опирающегося на ее, то есть угла NBA. Получаем NA=2*32=64. AB диаметр, значит дуга BN =180-NA=116. А угол NMB вписанный, и опирается на дугу BN, и равен ее половине, то есть 116/2=58.
Задание 2911
На окружности по разные стороны от диаметра $$AB$$ взяты точки $$M$$ и $$N$$. Известно, что $$\angle NBA = 46^\circ$$. Найдите угол $$NMB$$. Ответ дайте в градусах.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 3412
На окружности по разные стороны от диаметра $$AB$$ взяты точки $$M$$ и $$N$$. Известно, что $$\angle NBA = 44^\circ$$. Найдите угол $$NMB$$. Ответ дайте в градусах.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
- $$\angle NBA=\frac{1}{2}\cup AN\Rightarrow \cup AN=44^{\circ}\cdot 2=88^{\circ}$$ (вписанный угол)
- $$\cup NB=180^{\circ}-\cup NA=180^{\circ}-88^{\circ}=92^{\circ}$$ ($$AB$$ - диаметр)
- $$\angle NMB=\frac{1}{2}\cup NB=\frac{92^{\circ}}{2}=46^{\circ}$$ (вписанный угол)
