ОГЭ 2022. Вариант 6 Ященко 36 вариантов ФИПИ школе.
Решаем 6 вариант ОГЭ Ященко 2022 года сборника ФИПИ школе 36 вариантов. Полный разбор всего 6 варианта (всех заданий).
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 1-5
Счетчики
В жилых домах установлены бытовые электросчётчики, которые фиксируют расход электроэнергии в киловатт-часах (кВт • ч). Учёт расхода электроэнергии может быть однотарифным, двухтарифным или трёхтарифным.
При однотарифном учёте стоимость 1 кВт • ч электроэнергии не меняется в течение суток. При двухтарифном и трёхтарифном учёте она различна в зависимости от времени суток (сутки разбиты на периоды, называемые тарифными зонами).
В таблице дана стоимость 1 кВт*ч электроэнергии в рублях в 2021 году.
| I полугодие 2021 г. | II полугодие 2021 г. | |
| Однотарифный учёт | 5,47 | 5,66 |
| Двухтарифный учёт (распределение по двум тарифным зонам): | ||
| ночная зона Т2 (23:00-7:00) | 2,13 | 2,32 |
| дневная зона Т1 (7:00-23:00) | 6,29 | 6,51 |
| Трёхтарифный учёт (распределение по трём тарифным зонам): | ||
| ночная зона Т2 (23:00-7:00) | 2,13 | 2,32 |
| полупиковая зона ТЗ (10:00-17:00; 21:00-23:00) | 5,47 | 5,66 |
| пиковая зона Т1 (7:00-10:00; 17:00-21:00) | 6,57 | 6,79 |
В квартире у Петра Сергеевича установлен трёхтарифный счётчик, и в 2021 году Пётр Сергеевич оплачивал электроэнергию по трёхтарифному учёту.
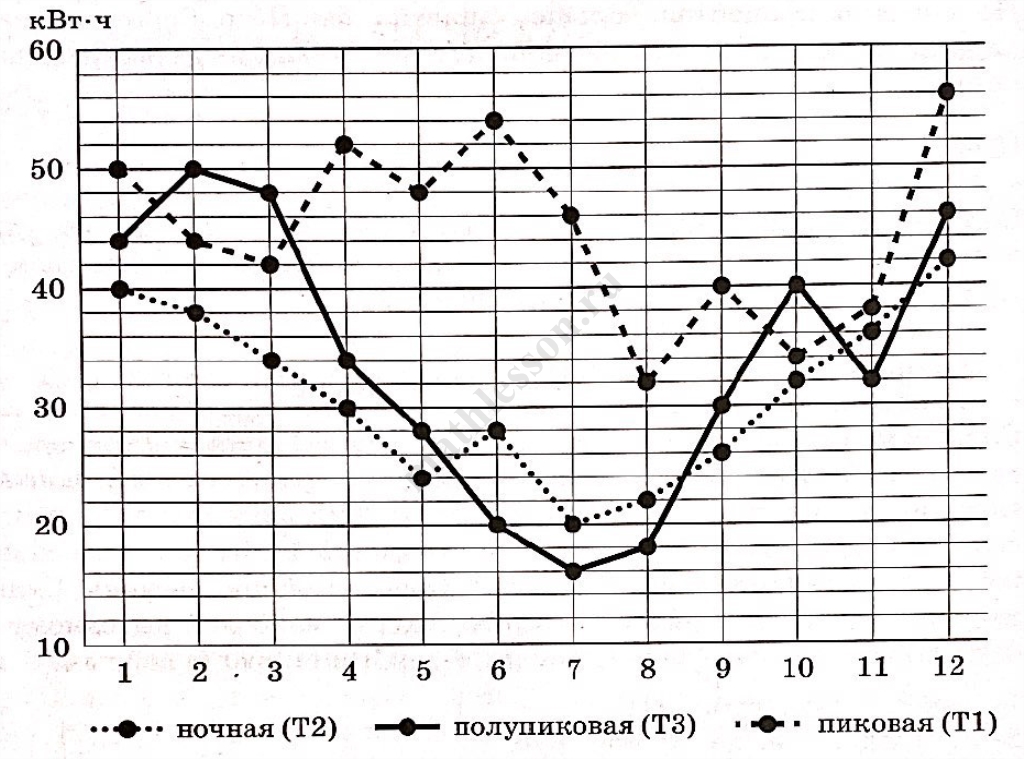
На рисунке точками показан расход электроэнергии в квартире Петра Сергеевича по тарифным зонам за каждый месяц 2021 года. Для наглядности точки соединены линиями.
1) Пользуясь рисунком, поставьте в соответствие каждому из указанных периодов времени характеристику расхода электроэнергии.
| ПЕРИОДЫ | ХАРАКТЕРИСТИКИ |
| A) февраль — март | 1) максимально уменьшился расход в пиковой зоне |
| Б) май — июнь | 2) расход уменьшился во всех трёх тарифных зонах, но больше всего — в ночной зоне |
| B) июль — август | 3) расход в пиковой и ночной зонах увеличился одинаково |
| Г) октябрь — ноябрь | 4) расход в полупиковой зоне уменьшился, а в пиковой и ночной — увеличился |
В таблице под каждой буквой укажите соответствующий номер
| А | Б | В | Г |
2) В каком месяце 2021 года расход электроэнергии был наименьшим? Запишите в ответ расход электроэнергии (в кВт • ч) в этом месяце.
3) Сколько рублей должен был бы заплатить Пётр Сергеевич за электроэнергию, израсходованную в июне, если бы пользовался однотарифным учётом?
4) На сколько процентов больше заплатил бы Пётр Сергеевич за электроэнергию, израсходованную в марте, если бы пользовался двухтарифным учётом? Ответ округлите до десятых.
5) Соседи Николая Андреевича, семья Сидоровых, исходя из данных по расходу электроэнергии за 2021 год в своей квартире, рассчитали средний расход электроэнергии за месяц по тарифным зонам:
Сидоровы предполагают, что в 2022 году средний расход электроэнергии будет таким же. Исходя из этого, выберите наиболее выгодный вариант учёта электроэнергии для семьи Сидоровых в 2022 году (однотарифный, двухтарифный или трёхтарифный). Считайте, что стоимость 1 кВт • ч электроэнергии будет такой же, как во П полугодии 2021 года. Оцените общие расходы Сидоровых на оплату электроэнергии (в рублях) за 2022 год (по наиболее выгодному варианту учёта), если средний расход электроэнергии действительно будет таким же.
В ответ запишите номер верного варианта оценки расходов.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 6
Найдите значение выражения $$(\frac{2}{15}+\frac{5}{12})\cdot \frac{16}{11}$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 9
Решите уравнение: $$x^2 - 4 = 2x - 1$$. Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 10
Вероятность того, что новая шариковая ручка пишет плохо (или не пишет), равна $$0,14$$. Покупатель в магазине выбирает одну шариковую ручку. Найдите вероятность того, что эта ручка пишет хорошо.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 12
Потенциальная энергия тела (в джоулях) в поле тяготения Земли вблизи её поверхности вычисляется по формуле $$E = mgh$$, где $$m$$ — масса тела (в килограммах), $$g$$ — ускорение свободного падения (в м/с²), а $$h$$ — высота (в метрах), на которой находится это тело относительно поверхности. Пользуясь этой формулой, найдите $$m$$ (в килограммах), если $$g = 9{,}8$$ м/с², $$h = 5$$ м, а $$E = 196$$ Дж.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 15
В треугольнике $$ABC$$ угол $$C = 90^\circ$$, $$M$$ — середина стороны $$AB$$, $$AB = 64$$, $$BC = 44$$. Найдите $$CM$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 16
Касательные в точках $$A$$ и $$B$$ к окружности с центром в точке $$O$$ пересекаются под углом $$56^\circ$$. Найдите угол $$ABO$$. Ответ дайте в градусах.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 17
Высота равнобедренной трапеции, проведённая из вершины $$C$$, делит основание $$AD$$ на отрезки длиной $$8$$ и $$17$$. Найдите длину основания $$BC$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 19
Какое из следующих утверждений верно?
- Диагонали ромба равны.
- Отношение площадей подобных треугольников равно коэффициенту подобия.
- В треугольнике против большего угла лежит большая сторона.
В ответ запишите номер выбранного утверждения.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 20
Решите систему уравнений: $$\left\{\begin{aligned} x^2 + y^2 = 65 \\ xy = 8 \end{aligned}\right.$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


1) Из второго уравнения: $$y = \dfrac{8}{x},\quad x \neq 0.$$ Подставим в первое: $$x^2 + \left(\dfrac{8}{x}\right)^2 = 65.$$ Умножим на $$x^2$$: $$x^4 + 64 = 65x^2.$$ Переносим всё в одну сторону: $$x^4 - 65x^2 + 64 = 0.$$ Обозначим $$t = x^2$$: $$t^2 - 65t + 64 = 0.$$
2) Найдём корни через дискриминант: $$D = 65^2 - 4\cdot 1\cdot 64 = 4225 - 256 = 3969.$$ $$t_{1,2} = \dfrac{65 \pm \sqrt{3969}}{2} = \dfrac{65 \pm 63}{2}.$$ Тогда $$t_1 = \dfrac{65 + 63}{2} = 64,\qquad t_2 = \dfrac{65 - 63}{2} = 1.$$ То есть $$x^2 = 64 \Rightarrow x = \pm 8,\qquad x^2 = 1 \Rightarrow x = \pm 1.$$
3) Найдём $$y = \dfrac{8}{x}.$$
Если $$x = 8,$$ то $$y = 1.$$
Если $$x = -8,$$ то $$y = -1.$$
Если $$x = 1,$$ то $$y = 8.$$
Если $$x = -1,$$ то $$y = -8.$$
Решения системы: $$(1;8),\ (-1;-8),\ (8;1),\ (-8;-1).$$
Задание 21
Первый рабочий за час делает на $$6$$ деталей больше, чем второй, и выполняет заказ, состоящий из $$140$$ деталей, на $$3$$ часа быстрее, чем второй рабочий, выполняющий такой же заказ. Сколько деталей в час делает первый рабочий?
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 23
Отрезки $$AB$$ и $$DC$$ лежат на параллельных прямых, а отрезки $$AC$$ и $$BD$$ пересекаются в точке $$M$$. Найдите $$MC$$, если $$AB=15$$, $$DC=30$$, $$AC=39$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!