ОГЭ 2023. Вариант 16 Ященко 36 вариантов ФИПИ школе.
Решаем 16 вариант ОГЭ Ященко 2023 года сборника ФИПИ школе 36 вариантов. Полный разбор всего 16 варианта (всех заданий) Ященко 2023 ФИПИ 36 вариантов.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 1-5
Счетчики
В жилых домах установлены бытовые электросчётчики, которые фиксируют расход электроэнергии в киловатт-часах (кВт • ч). Учёт расхода электроэнергии может быть однотарифным, двухтарифным или трёхтарифным.
При однотарифном учёте стоимость 1 кВт • ч электроэнергии не меняется в течение суток. При двухтарифном и трёхтарифном учёте она различна в зависимости от времени суток (сутки разбиты на периоды, называемые тарифными зонами).
В таблице дана стоимость 1 кВт*ч электроэнергии в рублях в 2021 году.
| I полугодие 2021 г. | II полугодие 2021 г. | |
| Однотарифный учёт | 5,47 | 5,66 |
| Двухтарифный учёт (распределение по двум тарифным зонам): | ||
| ночная зона Т2 (23:00-7:00) | 2,13 | 2,32 |
| дневная зона Т1 (7:00-23:00) | 6,29 | 6,51 |
| Трёхтарифный учёт (распределение по трём тарифным зонам): | ||
| ночная зона Т2 (23:00-7:00) | 2,13 | 2,32 |
| полупиковая зона ТЗ (10:00-17:00; 21:00-23:00) | 5,47 | 5,66 |
| пиковая зона Т1 (7:00-10:00; 17:00-21:00) | 6,57 | 6,79 |
В квартире у Петра Сергеевича установлен трёхтарифный счётчик, и в 2021 году Пётр Сергеевич оплачивал электроэнергию по трёхтарифному учёту.
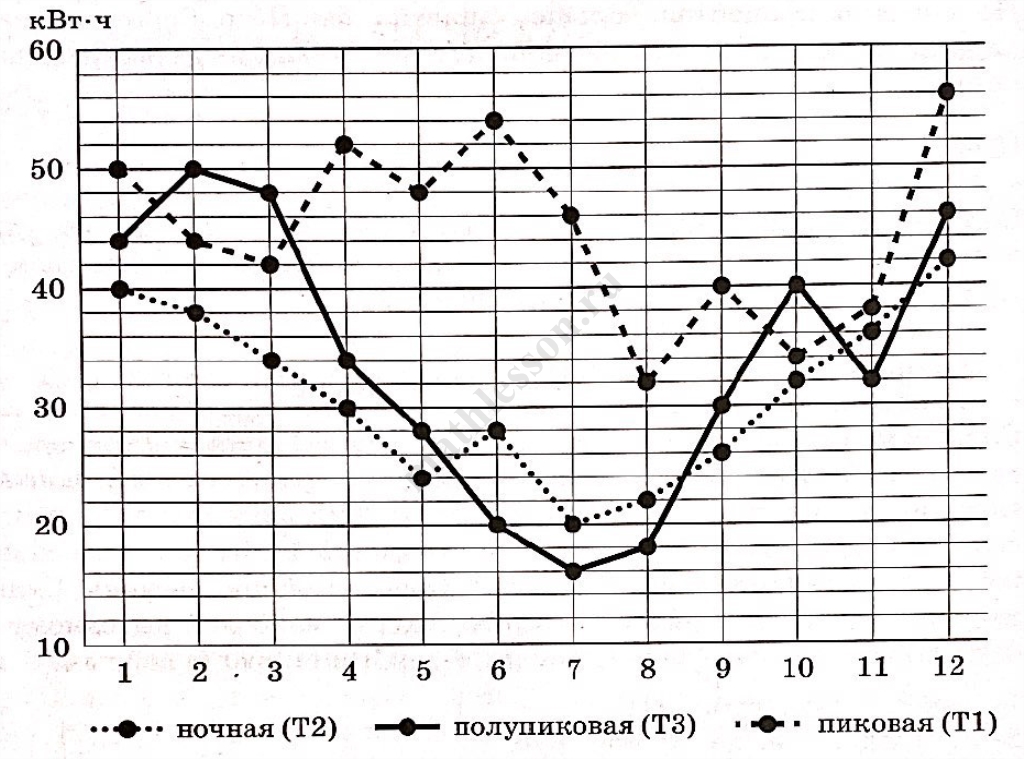
На рисунке точками показан расход электроэнергии в квартире Петра Сергеевича по тарифным зонам за каждый месяц 2021 года. Для наглядности точки соединены линиями.
1) Пользуясь рисунком, поставьте в соответствие каждому из указанных периодов времени характеристику расхода электроэнергии.
| ПЕРИОДЫ | ХАРАКТЕРИСТИКИ |
| A) февраль — март | 1) максимально уменьшился расход в пиковой зоне |
| Б) май — июнь | 2) расход уменьшился во всех трёх тарифных зонах, но больше всего — в ночной зоне |
| B) июль — август | 3) расход в пиковой и ночной зонах увеличился одинаково |
| Г) октябрь — ноябрь | 4) расход в полупиковой зоне уменьшился, а в пиковой и ночной — увеличился |
В таблице под каждой буквой укажите соответствующий номер
| А | Б | В | Г |
2) В каком месяце 2021 года расход электроэнергии был наименьшим? Запишите в ответ расход электроэнергии (в кВт • ч) в этом месяце.
3) Сколько рублей должен был бы заплатить Пётр Сергеевич за электроэнергию, израсходованную в июне, если бы пользовался однотарифным учётом?
4) На сколько процентов больше заплатил бы Пётр Сергеевич за электроэнергию, израсходованную в марте, если бы пользовался двухтарифным учётом? Ответ округлите до десятых.
5) Соседи Николая Андреевича, семья Сидоровых, исходя из данных по расходу электроэнергии за 2021 год в своей квартире, рассчитали средний расход электроэнергии за месяц по тарифным зонам:
Сидоровы предполагают, что в 2022 году средний расход электроэнергии будет таким же. Исходя из этого, выберите наиболее выгодный вариант учёта электроэнергии для семьи Сидоровых в 2022 году (однотарифный, двухтарифный или трёхтарифный). Считайте, что стоимость 1 кВт • ч электроэнергии будет такой же, как во П полугодии 2021 года. Оцените общие расходы Сидоровых на оплату электроэнергии (в рублях) за 2022 год (по наиболее выгодному варианту учёта), если средний расход электроэнергии действительно будет таким же.
В ответ запишите номер верного варианта оценки расходов.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 6
Найдите значение выражения $$(\frac{2}{15}+\frac{5}{12})\cdot \frac{16}{11}$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 9
Решите уравнение: $$x^2 - 4 = 2x - 1$$. Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 10
Вероятность того, что новая шариковая ручка пишет плохо (или не пишет), равна $$0,14$$. Покупатель в магазине выбирает одну шариковую ручку. Найдите вероятность того, что эта ручка пишет хорошо.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 12
Потенциальная энергия тела (в джоулях) в поле тяготения Земли вблизи её поверхности вычисляется по формуле $$E = mgh$$, где $$m$$ — масса тела (в килограммах), $$g$$ — ускорение свободного падения (в м/с²), а $$h$$ — высота (в метрах), на которой находится это тело относительно поверхности. Пользуясь этой формулой, найдите $$m$$ (в килограммах), если $$g = 9{,}8$$ м/с², $$h = 5$$ м, а $$E = 196$$ Дж.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 15
В треугольнике $$ABC$$ угол $$C = 90^\circ$$, $$M$$ — середина стороны $$AB$$, $$AB = 64$$, $$BC = 44$$. Найдите $$CM$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 16
Касательные в точках $$A$$ и $$B$$ к окружности с центром в точке $$O$$ пересекаются под углом $$56^\circ$$. Найдите угол $$ABO$$. Ответ дайте в градусах.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 17
Высота равнобедренной трапеции, проведённая из вершины $$C$$, делит основание $$AD$$ на отрезки длиной $$8$$ и $$17$$. Найдите длину основания $$BC$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 19
Какое из следующих утверждений верно?
- Диагонали ромба равны.
- Отношение площадей подобных треугольников равно коэффициенту подобия.
- В треугольнике против большего угла лежит большая сторона.
В ответ запишите номер выбранного утверждения.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 20
Решите систему уравнений: $$\left\{\begin{aligned} x^2 + y^2 = 65 \\ xy = 8 \end{aligned}\right.$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


1) Из второго уравнения: $$y = \dfrac{8}{x},\quad x \neq 0.$$ Подставим в первое: $$x^2 + \left(\dfrac{8}{x}\right)^2 = 65.$$ Умножим на $$x^2$$: $$x^4 + 64 = 65x^2.$$ Переносим всё в одну сторону: $$x^4 - 65x^2 + 64 = 0.$$ Обозначим $$t = x^2$$: $$t^2 - 65t + 64 = 0.$$
2) Найдём корни через дискриминант: $$D = 65^2 - 4\cdot 1\cdot 64 = 4225 - 256 = 3969.$$ $$t_{1,2} = \dfrac{65 \pm \sqrt{3969}}{2} = \dfrac{65 \pm 63}{2}.$$ Тогда $$t_1 = \dfrac{65 + 63}{2} = 64,\qquad t_2 = \dfrac{65 - 63}{2} = 1.$$ То есть $$x^2 = 64 \Rightarrow x = \pm 8,\qquad x^2 = 1 \Rightarrow x = \pm 1.$$
3) Найдём $$y = \dfrac{8}{x}.$$
Если $$x = 8,$$ то $$y = 1.$$
Если $$x = -8,$$ то $$y = -1.$$
Если $$x = 1,$$ то $$y = 8.$$
Если $$x = -1,$$ то $$y = -8.$$
Решения системы: $$(1;8),\ (-1;-8),\ (8;1),\ (-8;-1).$$
Задание 21
Первый рабочий за час делает на $$6$$ деталей больше, чем второй, и выполняет заказ, состоящий из $$140$$ деталей, на $$3$$ часа быстрее, чем второй рабочий, выполняющий такой же заказ. Сколько деталей в час делает первый рабочий?
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 23
Отрезки $$AB$$ и $$DC$$ лежат на параллельных прямых, а отрезки $$AC$$ и $$BD$$ пересекаются в точке $$M$$. Найдите $$MC$$, если $$AB=15$$, $$DC=30$$, $$AC=39$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!