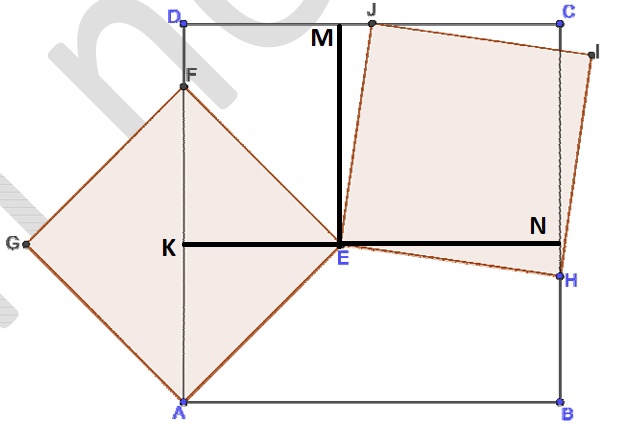
Задание 813
Задание 813
Дан квадрат $$ABCD$$. Построены два равных друг другу квадрата $$AEFG$$ и $$HIJE$$ таким образом, что точки $$H$$ и $$J$$ лежат на сторонах $$BC$$ и $$CD$$ квадрата $$ABCD$$ соответственно. Найдите сумму длин отрезков $$DJ$$ и $$BH$$, если известно, что $$AG = 4\sqrt{2}$$.
Пусть $$EK\perp AD; EN\perp CB; EM\perp DC.$$ Тогда:
$$\Delta EMJ=\Delta ENH$$ (по гипотенузе и острому углу) $$\Rightarrow MJ=NH=x.$$
$$EK=KA=\frac{AF}{2}=\frac{4\sqrt{2}\cdot\sqrt{2}}{2}=4=NB=DM.$$
Тогда $$DJ+BH=DM+MJ+BN-NH=4+x-x+4=8.$$
Аналоги к этому заданию:
Задание 676
Дан правильный треугольник $$ABC$$. На стороне $$AB$$ взята точка $$D$$. Через точки $$A$$, $$C$$ и $$D$$ проведена окружность $$\omega$$. Площадь круга, ограниченного окружностью $$\omega$$, равна $$27\pi$$. Найдите длину отрезка $$CD$$.
$$S=\pi R^2=27\pi\Rightarrow R=\sqrt{27}=3\sqrt{3}$$ - радиус описанной окружности около $$\Delta ACD$$
$$\frac{CD}{2\sin A}=R\Rightarrow CD=R\cdot2\sin A=3\sqrt{3}\cdot2\cdot\frac{\sqrt{3}}{2}=9$$
Задание 694
Даны три равных друг другу прямоугольника $$ABCD$$, $$BFGE$$, $$HGJI$$. При этом точки $$E$$ и $$H$$ лежат на отрезках $$CB$$ и $$EG$$ соответственно (см. рис.). Найдите градусную меру угла $$BID$$.
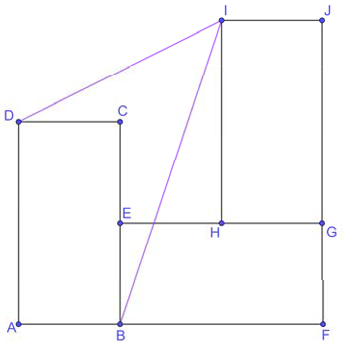
Пусть $$DC=EB=HG=x; AD=EG=IH=y.$$ Тогда $$EH=EG-HG=y-x.$$ Пусть $$DC\cap IH=L.$$
Тогда $$CL=EH=y-x,$$ но $$DL=x+y-x=y.$$
Тогда $$DI=\sqrt{DL^2+LI^2}=\sqrt{y^2+x^2}$$
$$(CE=y-x=HL\Rightarrow LI=y-(y-x)=x)$$
$$DB=\sqrt{x^2+y^2}.$$ Получим $$DI=DB.$$
При этом $$\Delta ADB=\Delta DLI.$$ Тогда $$\angle ADB=\angle IDL.$$
Следовательно, $$\angle IDB=\angle ADC=90^{\circ}\Rightarrow\angle BID=\frac{90^{\circ}}{2}=45^{\circ}.$$
Задание 783
Дан полукруг диаметром $$AB$$ площадью $$50\pi$$. Три равных друг другу прямоугольных треугольника $$ACD$$, $$DCE$$ и $$DFG$$ расположены таким образом, что точки $$C$$ и $$E$$ лежат на отрезке $$AB$$, а точка $$G$$ лежит на полуокружности диаметром $$AB$$ (см. рис.). Найдите длину отрезка $$DE$$.
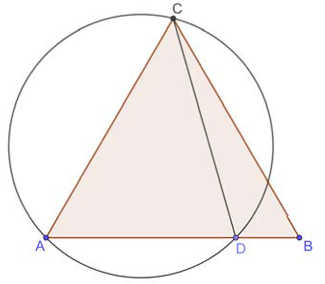
$$S=\frac{\pi R^2}{2}=\pi\cdot50\Rightarrow R^2=100\Rightarrow R=10\Rightarrow AB=20.$$
Опустим из G перпендикуляр на AB; пусть он пересекает $$AB=H.$$ Тогда $$AC=CE=x; EH=HB=y.$$
Или $$2x+2y=20\Rightarrow x+y=10.$$
Но DGHC - прямоугольник $$\Rightarrow DG=CH=x+y=10\Rightarrow DE=DG=10.$$
Задание 797
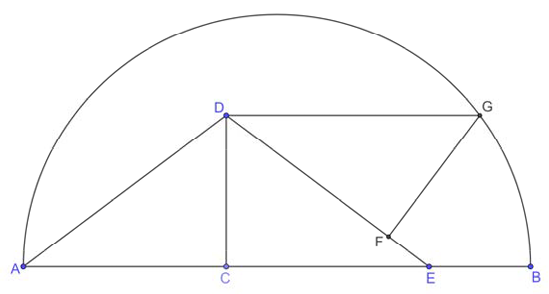
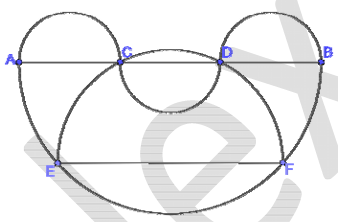
Дан полукруг диаметром $$AB$$ и три равных друг другу полукруга диаметрами $$AC$$, $$CD$$ и $$DB$$ (см. рис.). На полуокружности диаметром $$AB$$ взяты точки $$E$$ и $$F$$ так, что полуокружность диаметром $$EF$$ проходит через точки $$C$$ и $$D$$. Найдите площадь полукруга диаметром $$EF$$, если $$AC = \frac{4}{\sqrt{\pi}}$$.
Пусть O - середина EF, Q - середина CD, $$EO=OF=R, AC=CD=DB=r=\frac{4}{\sqrt{\pi}}.$$ В треугольнике EOQ по теореме Пифагора:
$$(\frac{3r}{2})^2=R^2+OQ^2 \Leftrightarrow OQ^2=\frac{9r^2}{4}-R^2. \quad \quad(1)$$
В треугольнике DQO по теореме Пифагора:
$$OQ^2+(\frac{r}{2})^2=R^2 \quad \quad(2)$$
Подставляя (1) в (2), получим:
$$\frac{9r^2}{4}-R^2+(\frac{r}{2})^2=R^2 \Leftrightarrow R^2= \frac {5r^2}{4} \quad \quad(3)$$
С учётом (3) искомая площадь S:
$$S=\frac {\pi R^2}{2} = \frac{\pi}{2} \cdot \frac {5r^2}{4} = \frac{5\pi}{8} \cdot \frac{16}{\pi} =10.$$