ОГЭ 2022. Вариант 1 Ященко 36 вариантов ФИПИ школе.
Решаем 1 вариант ОГЭ Ященко 2022 года сборника ФИПИ школе 36 вариантов. Полный разбор всего 1 варианта (всех заданий).
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 1-5
Печи
Хозяин дачного участка строит баню с парным отделением. Парное отделение имеет размеры: длина $$3,5$$ м, ширина $$2,2$$ м, высота $$2$$ м. Окон в парном отделении нет, для доступа внутрь планируется дверь шириной $$60$$ см, высота дверного проёма $$1,8$$ м. Для прогрева парного отделения можно использовать электрическую или дровяную печь. В таблице представлены характеристики трёх печей.
| номер печи | тип | объем помещения (куб. м) | масса (кг) | стоимость (руб.) |
| 1 | дровяная | 8-12 | 40 | 18000 |
| 2 | дровяная | 10-16 | 48 | 19500 |
| 3 | электрическая | 9-15,5 | 15 | 15000 |
Для установки дровяной печи дополнительных затрат не потребуется. Установка электрической печи потребует подведения специального кабеля, что обойдётся в $$5700$$ руб.
1. Установите соответствие между массами и номерами печей. Заполните таблицу, в бланк ответов перенесите последовательность трёх цифр без пробелов, запятых и других дополнительных символов.
| масса (кг) | 15 | 40 | 48 |
| номер печи |
2. Найдите суммарную площадь стен парного отделения строящейся бани (без площади двери). Ответ дайте в квадратных метрах.
3. На сколько рублей покупка дровяной печи, подходящей по объёму парного отделения, обойдётся дешевле электрической с учётом установки?
4. В прошлом году печи, указанные в таблице, стоили дороже. На них были сделаны скидки: на печь помер 1 скидка составила 10%, на печь номер $$2$$ — $$35 %$$ , на печь номер $$3$$ — $$25 %$$. Сколько рублей стоила печь номер $$1$$ в прошлом году?
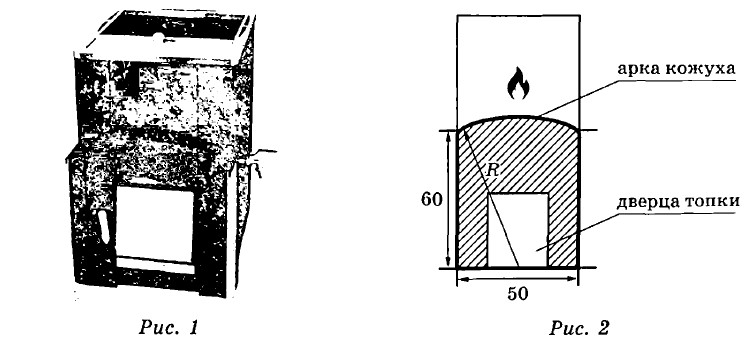
5. Хозяин выбрал дровяную печь (рис. 1). Чертёж передней панели печи показан на рисунке 2.
Печь снабжена кожухом вокруг дверцы топки. Верхняя часть кожуха выполнена в виде арки, приваренной к передней стенке печки по дуге окружности с центром в середине нижней части кожуха (рис. 2). Для установки печки хозяину понадобилось узнать радиус закругления арки $$R$$. Размеры кожуха в сантиметрах показаны на рисунке. Найдите радиус закругления арки в сантиметрах.
Задание 7
Какое из данных ниже чисел принадлежит отрезку $$[8; 9]$$?
1) $$\frac{46}{7}$$
2) $$\frac{53}{7}$$
3) $$\frac{55}{7}$$
4) $$\frac{61}{7}$$
В ответе запишите номер правильного варианта ответа.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Отрезок $$[8; 9]$$ можно представить в виде дробей со знаменателем $$7,$$ следующим образом:
$$[\frac{8\cdot7}{7};\frac{9\cdot7}{7}]=[\frac{56}{7};\frac{63}{7}]$$
Отсюда хорошо видно, что дробь $$\frac{61}{7}$$ принадлежит этому интервалу.
Задание 9
Решите уравнение: $$x^2 - 64 = 0$$. Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 12
Энергия заряженного конденсатора $$W$$ (в Дж) вычисляется по формуле $$W = \frac{CU^2}{2}$$, где $$C$$ — ёмкость конденсатора (в Ф), а $$U$$ — разность потенциалов на обкладках конденсатора (в В). Найдите энергию конденсатора (в Дж) ёмкостью $$10^{-4}$$ Ф, если разность потенциалов на обкладках конденсатора равна $$16$$ В.
Задание 14
В амфитеатре $$14$$ рядов. В первом ряду $$20$$ мест, а в каждом следующем — на $$3$$ места больше, чем в предыдущем. Сколько мест в десятом ряду амфитеатра?
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 18
На клетчатой бумаге с размером клетки $$1 \times 1$$ изображена трапеция. Найдите длину её средней линии.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 20
Решите уравнение: $$x^2 - 2x + \sqrt{6 - x} = \sqrt{6 - x} + 35$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
1) ОДЗ: $$6 - x \ge 0 \;\Rightarrow\; x \le 6.$$
2) Перенесём одинаковые корни в одну сторону: $$x^2 - 2x + \sqrt{6 - x} = \sqrt{6 - x} + 35,$$ $$x^2 - 2x = 35,$$ $$x^2 - 2x - 35 = 0.$$
3) Решим квадратное уравнение: $$D = (-2)^2 - 4\cdot 1\cdot(-35) = 4 + 140 = 144,$$ $$x_{1,2} = \dfrac{2 \pm \sqrt{144}}{2} = \dfrac{2 \pm 12}{2}.$$ Получаем: $$x_1 = 7,\quad x_2 = -5.$$ С учётом условия $$x \le 6$$ подходит только $$x = -5.$$
Задание 21
Теплоход проходит по течению реки до пункта назначения $$216$$ км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна $$5$$ км/ч, стоянка длится $$5$$ часа, а в пункт отправления теплоход возвращается через $$23$$ часов после отплытия из него.
Задание 23
Прямая, параллельная основаниям трапеции $$ABCD$$, пересекает её боковые стороны $$AB$$ и $$CD$$ в точках $$E$$ и $$F$$ соответственно. Найдите длину отрезка $$EF$$, если $$AD=35$$, $$BC=21$$, $$CF:DF=5:2$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 24
Через точку $$O$$ пересечения диагоналей параллелограмма $$ABCD$$ проведена прямая, пересекающая стороны $$AB$$ и $$CD$$ в точках $$E$$ и $$F$$ соответственно. Докажите, что отрезки $$AE=CF$$.
Треугольники AOE и COF равны по стороне и двум прилежащим к ней углам: AO = CO, поскольку диагонали параллелограмма точкой пересечения делятся пополам, $$\angle AOE=\angle COF$$ как вертикальные, $$\angle OAE=\angle OCF$$ как накрест лежащие углы при пересечении параллельных прямых AB и CD секущей AC. Из равенства треугольников следует равенство их сходственных сторон: AE = CF. Что и требовалось доказать.