ОГЭ 2023. Вариант 2 Ященко 36 вариантов ФИПИ школе.
Решаем 2 вариант ОГЭ Ященко 2023 года сборника ФИПИ школе 36 вариантов. Полный разбор всего 2 варианта (всех заданий).
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 1-5
Теплицы
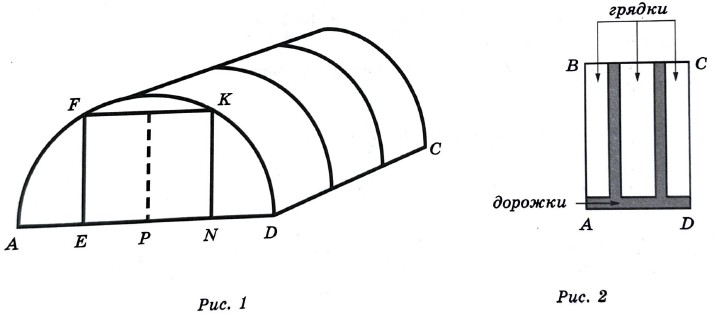
Глеб Сергеевич начал строить на дачном участке теплицу длиной 5 метров ( $$DC$$ на рис. 1). Для этого он сделал прямоугольный фундамент (рис. 2). Для каркаса теплицы нужно заказать металлические дуги в форме полуокружностей длиной 6 м каждая и покрытие для обтяжки теплицы. Отдельно требуется купить плёнку для передней и задней стенок теплицы. В передней стенке планируется вход, показанный на рис. 1 прямоугольником $$EFKN$$, где точки $$E, P$$ и $$N$$ делят отрезок $$AD$$ на равные части.
Внутри теплицы Глеб Сергеевич планирует сделать три грядки, как показано на рис. 2. Между грядками и при входе в теплицу будут дорожки шириной 40 см, для которых надо купить тротуарную плитку размером $$20 \times 20$$ см.
- Какое наименьшее количество дуг нужно заказать, чтобы расстояние между соседними дугами было не более 70 см?
- Найдите ширину теплицы в метрах с точностью до десятых.
- Сколько нужно купить упаковок плитки для дорожек, если в каждой упаковке 8 штук.
- Найдите площадь участка внутри теплицы, отведённого под грядки, в квадратных метрах. Результат округлите до десятых.
- Найдите высоту $$EF$$ входа в теплицу в сантиметрах с точностью до целого.
Задание 6
Найдите значение выражения $$(2\cdot 10^{2})^{4}\cdot (19\cdot 10^{-6})$$.
Задание 7
Какому из данных промежутков принадлежит число $$\frac{7}{11}$$?
1) $$[0,4; 0,5]$$
2) $$[0,5; 0,6]$$
3) $$[0,6; 0,7]$$
4) $$[0,7; 0,8]$$
Задание 8
Найдите значение выражения $$\sqrt{10 \cdot 7^2} \cdot \sqrt{10 \cdot 2^6}$$.
Задание 10
У бабушки $$20$$ чашек: $$11$$ с красными цветами, остальные с синими. Бабушка наливает чай в случайно выбранную чашку. Найдите вероятность того, что это будет чашка с синими цветами.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 12
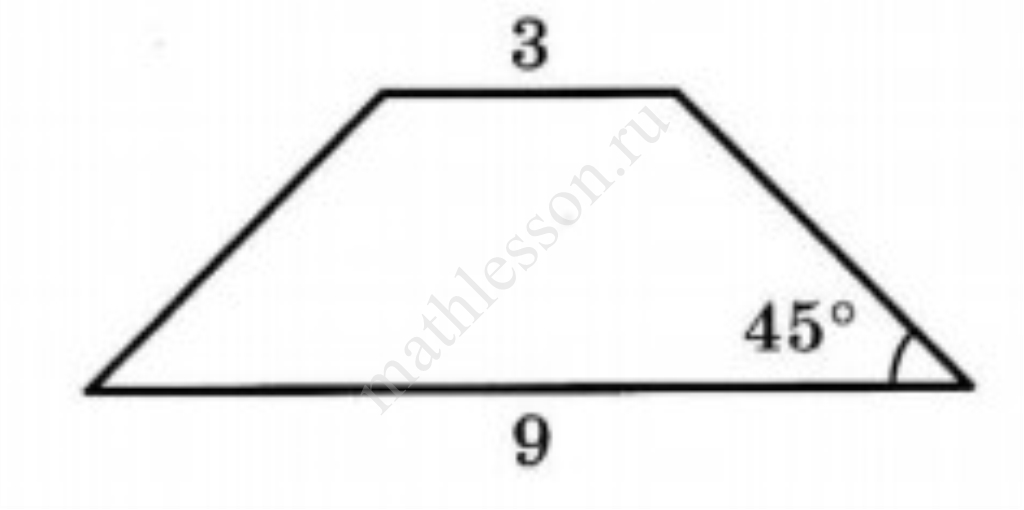
Площадь четырёхугольника можно вычислить по формуле $$S = \frac{d_1 d_2 \sin \alpha}{2}$$, где $$d_1$$ и $$d_2$$ — длины диагоналей четырёхугольника, $$\alpha$$ — угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали $$d_2$$, если $$d_1 = 9$$, $$\sin \alpha = \frac{5}{8}$$, $$S = 56,25$$.
Задание 14
В амфитеатре $$14$$ ряда, причём в каждом следующем ряду на одно и то же число мест больше, чем в предыдущем. В пятом ряду $$27$$ мест, а в восьмом ряду $$36$$ место. Сколько мест в последнем ряду амфитеатра?
Задание 16
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 19
Решите уравнение: $$(x + 2)^4 + (x + 2)^2 - 12 = 0$$
1) Замена: $$(x + 2)^2 = t.$$ Получаем $$t^2 + t - 12 = 0.$$
2) Дискриминант: $$D = 1^2 - 4\cdot 1\cdot(-12) = 1 + 48 = 49,$$ $$t_{1,2} = \dfrac{-1 \pm \sqrt{49}}{2} = \dfrac{-1 \pm 7}{2}.$$ Тогда $$t_1 = 3,\quad t_2 = -4.$$ Так как $$t = (x + 2)^2 \ge 0,$$ берём $$t = 3.$$
3) Возвращаемся к $$x$$: $$(x + 2)^2 = 3,$$ $$x + 2 = \pm \sqrt{3},$$ $$x = -2 \pm \sqrt{3}.$$
Задание 20
Первый велосипедист выехал из посёлка по шоссе со скоростью $$24$$ км/ч. Через час после него со скоростью $$21$$ км/ч из того же посёлка в том же направлении выехал второй велосипедист, а ещё через час — третий. Найдите скорость третьего велосипедиста, если сначала он догнал второго, а через $$9$$ часа после этого догнал первого.
Задание 24
В треугольнике $$ABC$$ известны длины сторон $$AB=12$$, $$AC=72$$, точка $$O$$ - центр окружности, описанной около треугольника $$ABC$$. Прямая $$BD$$, перпендикулярная прямой $$AO$$, пересекает сторону $$AC$$ в точке $$D$$. Найдите $$CD$$.