ОГЭ 2023. Вариант 14 Ященко 36 вариантов ФИПИ школе.
Решаем 14 вариант ОГЭ Ященко 2023 года сборника ФИПИ школе 36 вариантов. Полный разбор всего 14 варианта (всех заданий) Ященко 2023 ФИПИ 36 вариантов.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 1-5
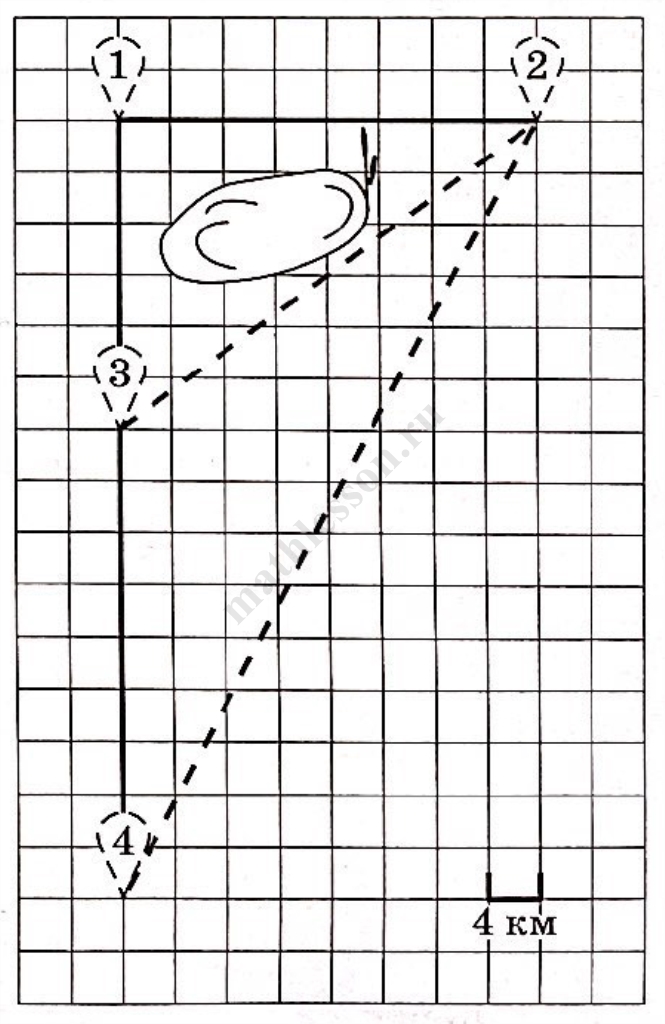
План местности
Володя летом отдыхает у дедушки в деревне Ёлочки. В воскресенье они собираются съездить на машине в село Кленовое. Из деревни Ёлочки в село Кленовое можно проехать по прямой грунтовой дороге. Есть более длинный путь: по прямолинейному шоссе через деревню Сосенки до деревни Жуки, где нужно повернуть под прямым углом направо на другое шоссе, ведущее в село Кленовое. Есть и третий маршрут: в деревне Сосенки можно свернуть на прямую грунтовую дорогу в село Кленовое, которая идёт мимо пруда.
Шоссе и грунтовые дороги образуют прямоугольные треугольники.
По шоссе Володя с дедушкой едут со скоростью 80 км/ч, а по грунтовой дороге — со скоростью 40 км/ч. На плане изображено взаимное расположение населённых пунктов, длина стороны каждой клетки равна 4 км.
1) Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты. Заполните таблицу, в бланк ответов перенесите последовательность трёх цифр без пробелов, запятых и других дополнительных символов.
| Насел, пункты | д. Ёлочки | с. Кленовое | д. Жуки |
| Цифры |
2) Сколько километров проедут Володя с дедушкой от деревни Ёлочки до села Кленового, если они поедут по шоссе через деревню Жуки?
3) Найдите расстояние от деревни Сосенки до села Кленового по прямой. Ответ дайте в километрах.
4) Сколько минут затратят на дорогу из деревни Ёлочки в село Кленовое Володя с дедушкой, если поедут через деревню Жуки?
5) В таблице указана стоимость (в рублях) некоторых продуктов в четырёх магазинах, расположенных в деревне Ёлочки, селе Кленовом, деревне Сосенки и деревне Жуки.
| Наименование продукта | д. Ёлочки | с. Кленовое | д. Сосенки | д. Жуки |
| Молоко (1л) | 42 | 45 | 38 | 43 |
| Хлеб (1 батон) | 22 | 25 | 23 | 27 |
| Сыр «Российский» (1 кг) | 320 | 290 | 270 | 280 |
| Говядина (1 кг) | 410 | 420 | 450 | 430 |
| Картофель (1 кг) | 26 | 18 | 24 | 16 |
Володя с дедушкой хотят купить 5 л молока, 3 кг сыра «Российский» и 4 кг картофеля.
В каком магазине такой набор продуктов будет стоить дешевле всего? В ответ запишите стоимость данного набора в этом магазине.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 7
Какое из следующих чисел заключено между числами $$3\sqrt{2}$$ и $$2\sqrt{3}$$?
1) $$2$$
2) $$3$$
3) $$4$$
4) $$5$$
В ответ запишите номер выбранного варианта.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 10
На тарелке лежат одинаковые на вид пирожки: $$4$$ с мясом, $$5$$ с рисом и $$21$$ с повидлом. Андрей наугад берёт один пирожок. Найдите вероятность того, что пирожок окажется с повидлом.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 12
В фирме «Эх, прокачу!» стоимость поездки на такси (в рублях) длительностью более $$5$$ минут рассчитывается по формуле $$C = 180 + 15 \cdot (t - 5)$$, где $$t$$ — длительность поездки (в минутах). Пользуясь этой формулой, рассчитайте стоимость $$16$$-минутной поездки. Ответ дайте в рублях.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 14
У Юли есть теннисный мячик. Она со всей силы бросила его об асфальт. После первого отскока мячик подлетел на высоту $$450$$ см, а после каждого следующего отскока от асфальта подлетал на высоту в $$3$$ раза меньше предыдущей. После какого по счёту отскока высота, на которую подлетит мячик, станет меньше $$20$$ см?
Задание 15
В треугольнике $$ABC$$ угол $$C = 90^\circ$$, $$BC = 15$$, $$AC = 3$$. Найдите $$\tan B$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 16
Угол $$A$$ трапеции $$ABCD$$ с основаниями $$AD$$ и $$BC$$, вписанной в окружность, равен $$76^\circ$$. Найдите угол $$C$$ этой трапеции. Ответ дайте в градусах.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 17
Две стороны параллелограмма равны $$7$$ и $$12$$, а один из углов этого параллелограмма равен $$30^\circ$$. Найдите площадь этого параллелограмма.
Задание 18
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 19
Какие из следующих утверждений верны?
- Один из углов треугольника всегда не превышает $$60^{\circ}$$ градусов.
- Средняя линия трапеции равна сумме её оснований.
- Касательная к окружности перпендикулярна радиусу, проведённому в точку касания.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Задание 20
Решите неравенство: $$(2x - 5)^2 \le (5x - 2)^2$$
1) Перенесём всё в левую часть и раскроем разность квадратов: $$(2x - 5)^2 - (5x - 2)^2 \le 0,$$ $$(2x - 5 - (5x - 2))(2x - 5 + (5x - 2)) \le 0.$$ Получаем $$(-3x - 3)(7x - 7) \le 0,$$ или $$-21(x + 1)(x - 1) \le 0.$$
2) Поделим обе части неравенства на $$-21$$ (знак неравенства меняется на противоположный): $$(x + 1)(x - 1) \ge 0.$$ Корни: $$x_1 = -1,\; x_2 = 1.$$ Отметим их на координатной прямой. Расставим знаки, которые принимает выражение $$(x + 1)(x - 1)$$ на полученных интервалах.
Знак произведения неотрицателен: $$x \in (-\infty; -1] \cup [1; +\infty).$$
Задание 21
Из $$A$$ в $$B$$ одновременно выехали два автомобилиста. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью $$55$$ км/ч, а вторую половину пути проехал со скоростью, большей скорости первого на $$6$$ км/ч, в результате чего прибыл в $$B$$ одновременно с первым автомобилистом. Найдите скорость первого автомобилиста.
Задание 22
Постройте график функции $$y = \left\{\begin{aligned} x^2 - 6x + 6, & x \geq 2; \\ x - 3, & x < 2 \end{aligned}\right.$$ Определите, при каких значениях $$m$$ прямая $$y = m$$ имеет с графиком ровно две общие точки.
Задание 23
В равнобедренной трапеции $$ABCD$$ с большим основанием $$AD$$ биссектриса угла $$A$$ пересекается с биссектрисой угла $$C$$ в точке $$F$$, а также пересекает сторону $$CD$$ в точке $$K$$. Известно, что прямые $$AB$$ и $$CF$$ параллельны. Найдите $$CF$$, если $$FK=4\sqrt{3}$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


- Пусть $$AF \cap BC=E$$. Так как ABCD – равнобедренная трапеция,$$\angle BAC+\angle BCD=180^{\circ}$$. Пусть $$\angle BAC=2\alpha\Rightarrow$$$$\angle BCD=180^{\circ}-2\alpha$$. Тогда $$\angle ECK=2\alpha$$, $$\angle CEK=\alpha$$ ($$\frac{\angle A}{2}$$ - как накрест лежащие)
- $$\angle AFC=\angle BAF=\alpha=\angle CFK$$ (накрест лежащие и вертикальные)
- $$\angle FCK=\frac{180^{\circ}-2\alpha}{2}=90^{\circ}-\alpha$$. Из треугольника CFK $$\angle CKF=180^{\circ}-(\alpha+90^{\circ}+\alpha)=90^{\circ}$$
- Из треугольника CKE: $$90^{\circ}+3\alpha=180^{\circ}\Rightarrow$$$$\alpha=30^{\circ}$$
- $$CF=\frac{FK}{\cos CFK}=$$$$\frac{4\sqrt{3}}{\frac{\sqrt{3}}{2}}=8$$
Задание 24
В выпуклом четырёхугольнике $$ABCD$$ углы $$DAC$$ и $$DBC$$ равны. Докажите, что углы $$CDB$$ и $$CAB$$ также равны.
Задание 25
Найдите площадь трапеции, диагонали которой равны $$17$$ и $$15$$, а средняя линия равна $$4$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!