Задание 1400
Задание 1400
Найдите площадь трапеции, диагонали которой равны $$10$$ и $$8$$, а средняя линия равна $$3$$.
Ответ: 24
Скрыть


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Скрыть
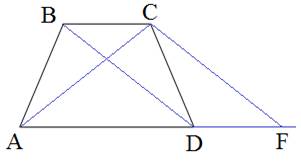
- Проведем из точки $$C$$ прямую, параллельную $$BD$$, пусть она пересекает $$AD$$ в точке $$K$$.
- $$BC\parallel DK ; BD\parallel CK \Rightarrow BCKD-$$ параллелограмм и $$BC=DK$$, $$BD=CK$$, $$AK=AD+DK=AD+BC$$.
- $$AD+BC=3\cdot 2=6$$ (удвоенная средняя линия)
- Пусть $$CH\perp AD: S_{ABCD}=\frac{BC+AD}{2} \cdot CH=\frac{1}{2} \cdot AK \cdot CH=S_{ACK}$$.
- $$p_{ACK}=\frac{10+8+6}{2}=12$$ По формуле Герона: $$S_{ACK}=\sqrt{12(12-10)(12-8)(12-6)}=\sqrt{12 \cdot 2 \cdot 4 \cdot 6}=\sqrt{12^2 \cdot 2^2}=24$$
Аналоги к этому заданию
Оригинал: 1400
Задание 2037
Найдите площадь трапеции, диагонали которой равны $$16$$ и $$12$$, а средняя линия равна $$10$$.
Ответ: 96
Скрыть


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Скрыть
- Проведем из С прямую, параллельную BD до пересечения с AD в F
- Средняя линия равна полусумме оснований, тогда: $$AD+BC=20$$
- BC параллельна DF, BD параллельна CF, тогда BCFD - параллелограмм, DF=BC, AF=20. При это площадь треугольников ABC и CDF равны (одинаковая высота и основания)
- Тогда площадь искомой трапеции равна площади треугольника ACF. Найдем ее по формуле Герона: $$p=\frac{16+12+20}{2}=24$$; $$S=\sqrt{24\cdot 8\cdot 12\cdot 4}=96$$
Оригинал: 1400
Задание 1390
Найдите площадь трапеции, диагонали которой равны $$17$$ и $$15$$, а средняя линия равна $$4$$.
Ответ: 60
Скрыть


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!