Задание 4906
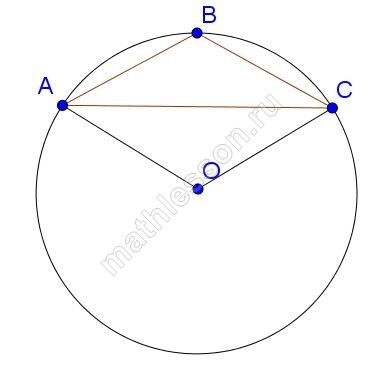
Боковая сторона равнобедренного треугольника равна $$5$$. Угол при вершине, противолежащий основанию, равен $$120^\circ$$. Найдите диаметр окружности, описанной около этого треугольника.
Пусть угол B равен 120 градусам, тогда $$\smile AC = 240^{\circ}$$ (по свойству вписанного угла), тогда меньшая дуга CA равна $$360-240=120^{\circ}$$, и центральный угол, опирающийся на эту дугу так же составляет 120 градусов ($$\angle AOC$$). Так как треугольники ABC и ACO равнобедренные, имею общую сторону и равные углы против этой стороны, то они между собой равны, следовательно, AO=5=r, где r - радиус окружности, следовательно, диаметр окружности равен 10
Задание 3177
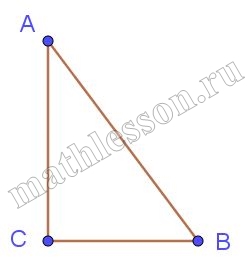
В треугольнике $$ABC$$ $$AC = \sqrt{5}$$, $$BC = \sqrt{11}$$, угол $$C = 90^\circ$$. Найдите радиус окружности, описанной около этого треугольника.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 4240
В треугольнике $$ABC$$ $$AC = 3\sqrt{7}$$, $$BC = 3\sqrt{2}$$, угол $$C$$ равен $$90^\circ$$. Найдите радиус окружности, описанной около этого треугольника.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Радиус описанной вокруг прямоугольного треугольника окружности равен половине длины его гипотенузы. Найдем гипотенузу по теореме Пифагора: $$AB=\sqrt{AC^{2}+BC^{2}}=\sqrt{9*7+9*2}=9$$ В таком случае радиус будет равен 9/2 = 4,5
Задание 3775
В треугольнике $$ABC$$ известно, что $$AC = 24$$, $$BC = \sqrt{265}$$, угол $$C = 90^\circ$$. Найдите радиус описанной окружности этого треугольника.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


По теореме Пифагора: $$AB=\sqrt{AC^{2}+BC^{2}}=\sqrt{576+265}=29$$. По свойству радиуса описанной окружности около прямоугольного треугольника : $$R=\frac{AB}{2}=14,5$$
Задание 2013
В треугольнике $$ABC$$ угол $$A$$ равен $$80^\circ$$, а угол $$B$$ равен $$40^\circ$$. Длина стороны $$AB$$ равна $$20\sqrt{3}$$. Найдите радиус окружности, описанной около треугольника $$ABC$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 4176
Окружность с центром в точке $$O$$ описана около равнобедренного треугольника $$ABC$$, в котором $$AB = BC$$ и $$\angle ABC = 138^\circ$$. Найдите величину угла $$BOC$$. Ответ дайте в градусах.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


$$\angle OBC=\frac{1}{2}\angle ABC=\frac{138^{\circ}}{2}=69^{\circ}$$
$$\bigtriangleup OBC$$ - равнобедренный, т.к. $$OB=OC$$ - радиусы $$\Rightarrow$$
$$\angle OCB=\angle OBC=69^{\circ}$$
$$\Rightarrow$$ $$\angle BOC=180-\angle OBC-\angle OCB=180^{\circ}-138^{\circ}=42^{\circ}$$
Задание 3200
Периметр треугольника равен $$56$$, одна из сторон равна $$19$$, а радиус вписанной в него окружности равен $$5$$. Найдите площадь этого треугольника.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Воспользуемся формулой площади треугольника через его полу периметр и радиус вписанной окружности: $$S=p*r$$; $$p=\frac{56}{2}=28$$. Тогда: $$S=28*5=140$$
Задание 2618
Площадь треугольника $$ABC$$ с внутренними углами $$\angle C = 90^\circ$$ и $$\angle B = 90^\circ$$ равна $$32\sqrt{3}$$. Найдите радиус окружности, описанной около треугольника $$ABC$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 1302
Прямоугольный треугольник с катетами $$5$$ см и $$12$$ см вписан в окружность. Чему равен радиус (в см) этой окружности?
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 1557
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 338
Радиус окружности, описанной около равностороннего треугольника, равен $$6\sqrt{3}$$. Найдите длину стороны этого треугольника.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 2170
Сторона $$AC$$ треугольника $$ABC$$ проходит через центр описанной около него окружности. Найдите $$\angle C$$, если $$\angle A = 44^\circ$$. Ответ дайте в градусах.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 4910
Сторона $$AC$$ треугольника $$ABC$$ проходит через центр описанной около него окружности. Найдите $$\angle C$$, если $$\angle A = 81^\circ$$. Ответ дайте в градусах.
Задание 4242
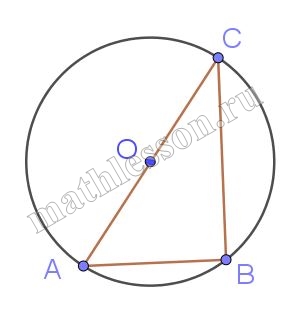
Треугольник $$ABC$$ вписан в окружность с центром в точке $$O$$. Точки $$O$$ и $$C$$ лежат в одной полуплоскости относительно прямой $$AB$$. Найдите угол $$ACB$$, если угол $$AOB$$ равен $$152^\circ$$. Ответ дайте в градусах.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Введем обозначения как показано на рисунке:
Угол AOB - центральный, значит его величина равна величине дуги на которую он опирается, то есть дуга AB = 152. Угол С - вписанный, его величина равна половине величины, на которую он опирается, то есть половину AB: 152/2=76