ОГЭ 2022. Вариант 35 Ященко 36 вариантов ФИПИ школе.
Решаем 35 вариант ОГЭ Ященко 2022 года сборника ФИПИ школе 36 вариантов. Полный разбор всего 35 варианта (всех заданий).
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 1-5
Теплицы
Сергей Петрович решил построить на дачном участке теплицу длиной 6 м. Для этого он сделал прямоугольный фундамент. Для каркаса теплицы Сергей Петрович заказал металлические дуги в форме полуокружностей длиной 5 м каждая и покрытие для обтяжки.
Отдельно требуется купить плёнку для передней и задней стенок теплицы. В передней стенке планируется вход, показанный на рисунке прямоугольником ВСС1В1, где точки В, О и С делят отрезок AD на четыре равные части. Внутри теплицы Сергей Петрович планирует сделать три грядки по длине теплицы — одну центральную широкую грядку и две узкие грядки по краям. Между грядками будут дорожки шириной 60 см, для которых необходимо купить тротуарную плитку размером 20 х 20 см.
1. Какое наименьшее количество дуг нужно заказать, чтобы расстояние между соседними дугами было не более 70 см?
2. Сколько упаковок плитки необходимо купить для дорожек между грядками, если она продаётся в упаковках по 8 штук?
3. Найдите ширину входа в теплицу. Ответ дайте в метрах с точностью до десятых.
4. Найдите ширину центральной грядки, если она в два раза больше ширины узкой грядки. Ответ дайте в сантиметрах с точностью до десятков.
5. Сколько процентов составляет площадь, отведённая под грядки, от площади всего участка, отведённого под теплицу? Ответ округлите до целых.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 8
Найдите значение выражения $$(\sqrt{32} - \sqrt{2}) \cdot \sqrt{2}$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 9
Решите уравнение: $$x^2 - 5x = 14$$. Если уравнение имеет более одного корня, в ответ запишите больший из корней.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 10
На семинар приехали $$5$$ учёных из Норвегии, $$6$$ из России и $$9$$ из Испании. Каждый учёный подготовил один доклад. Порядок докладов определяется случайным образом. Найдите вероятность того, что восьмым окажется доклад учёного из России.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 12
Кинетическая энергия тела вычисляется по формуле $$E = \frac{mv^2}{2}$$, где $$m$$ — масса тела (в килограммах), а $$v$$ — его скорость (в метрах в секунду). Пользуясь этой формулой, найдите $$E$$ (в джоулях), если $$v = 4$$ м/с и $$m = 9$$ кг.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 13
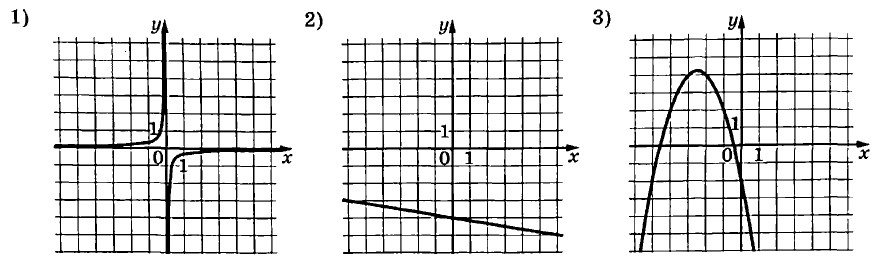
Укажите неравенство, которое не имеет решений:
1) $$x^2 - 3x - 11 0$$
2) $$x^2 - 3x + 11 0$$
3) $$x^2 - 3x + 11 > 0$$
4) $$x^2 - 3x - 11 > 0$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 14
В $$12:00$$ часы сломались и за каждый следующий час отставали на одно и то же количество минут по сравнению с предыдущим часом. В $$22:00$$ того же дня часы отставали на полчаса. На сколько минут отставали часы спустя $$15$$ часов после того, как они сломались?
Задание 15
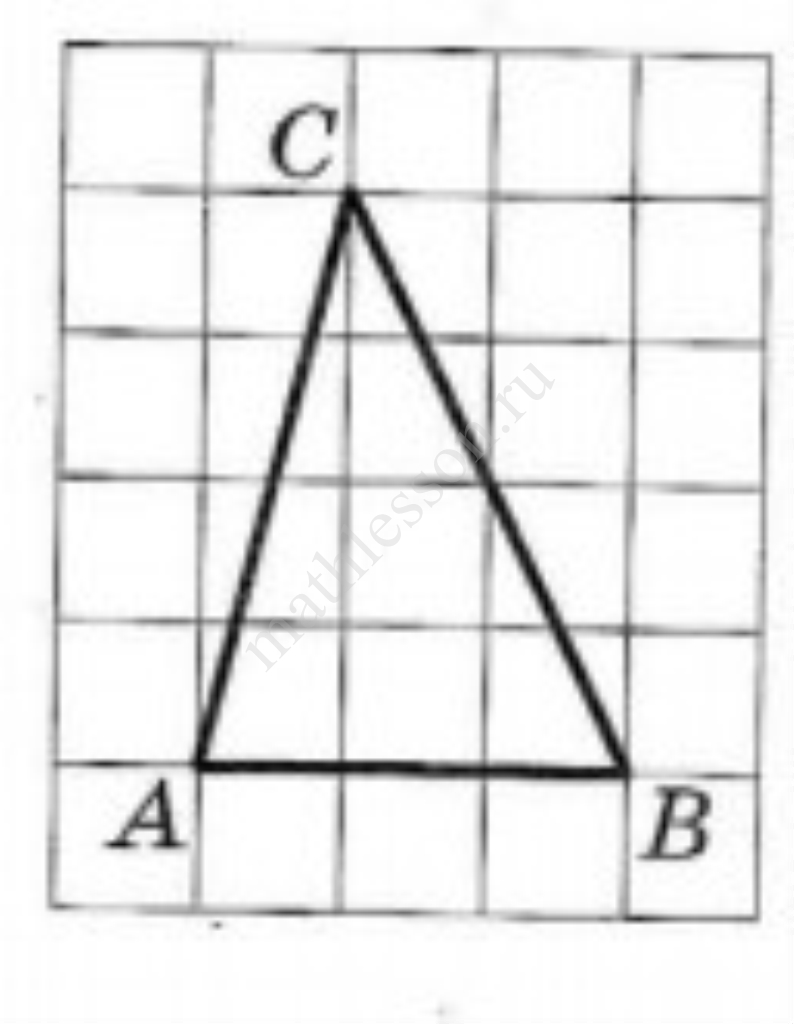
Синус острого угла $$A$$ треугольника $$ABC$$ равен $$\frac{\sqrt{7}}{4}$$. Найдите $$\cos A$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 16
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 19
Какие из следующих утверждений верны?
- Диагонали трапеции пересекаются и делятся точкой пересечения пополам.
- Все диаметры окружности равны между собой.
- Один из углов треугольника всегда не превышает $$60^{\circ}$$ градусов.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


1) Разложения:
$$50=2\cdot 5^2$$
Тогда: $$50^n=(2\cdot 5^2)^n=2^{n}\cdot 5^{2n}.$$ А также: $$2^{n-3}=2^{n-3}$$
2) Подставим: $$\frac{50^n}{5^{2n-1}\cdot 2^{n-3}} =$$$$\frac{2^{n}\cdot 5^{2n}}{5^{2n-1}\cdot 2^{n-3}}$$
3) Сократим: $$2^{n-(n-3)}\cdot 5^{2n-(2n-1)} =2^{3}\cdot 5^{1} =$$$$8\cdot 5=40$$
Задание 21
Первую половину пути автомобиль проехал со скоростью $$36$$ км/ч, а вторую половину – со скоростью $$99$$ км/ч. Найдите среднюю скорость (в км/ч) автомобиля на протяжении всего пути.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 22
Постройте график функции $$y = |x|x + |x| - 3x$$ и определите, при каких значениях $$m$$ прямая $$y = m$$ имеет с графиком ровно две общие точки.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!