Задание 271
Аналоги к этому заданию:
Задание 2535
В треугольнике $$ABC$$ биссектриса угла $$A$$ делит высоту, проведённую из вершины $$B$$, в отношении $$41:40$$, считая от точки $$B$$. Найдите радиус окружности, описанной около треугольника $$ABC$$, если $$BC=18$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 845
В треугольнике $$ABC$$ биссектриса угла $$A$$ делит высоту, проведённую из вершины $$B$$, в отношении $$5:4$$, считая от точки $$B$$. Найдите радиус окружности, описанной около треугольника $$ABC$$, если $$BC=12$$.
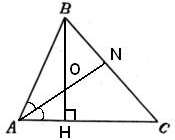
По условию задачи BO:OH=5:4, следовательно, OH:BO=4:5. По свойству биссектрисы AH:AB=HO:BO=4:5, но AH:AB – это косинус угла A, то есть $$\cos\angle A=\frac{4}{5}.$$ Рассмотрим прямоугольный треугольник AHB, в котором условно катет AH=4, а гипотенуза AB=5. По теореме Пифагора находим
$$BH=\sqrt{25-16}=3$$.
Тогда синус угла A равен $$\sin\angle A=\frac{3}{5}.$$ По следствию теоремы синусов имеем:
$$\frac{BC}{\sin A}=2R,$$
где R – радиус описанной окружности. Следовательно,
$$R=\frac{BC}{2\sin A}=\frac{12}{2\cdot0,6}=10.$$