ОГЭ 2023. Вариант 4 Ященко 36 вариантов ФИПИ школе.
Решаем 4 вариант ОГЭ Ященко 2023 года сборника ФИПИ школе 36 вариантов. Полный разбор всего 4 варианта (всех заданий).
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 1-5
Зонты
Две подруги Оля и Аня задумались о том, как рассчитать площадь поверхности зонта.
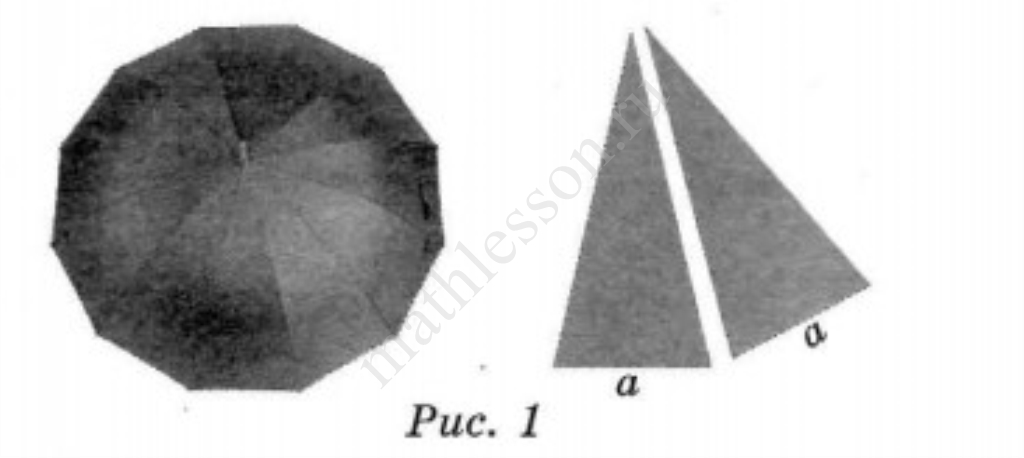
На первый взгляд зонт кажется круглым, а его купол напоминает часть сферы (сферический сегмент). Но если присмотреться, то видно, что купол зонта состоит из двенадцати отдельных клиньев, натянутых на каркас из двенадцати спиц (рис. 1). Сферическая форма в раскрытом состоянии достигается за счёт гибкости спиц и эластичности ткани, из которой изготовлен зонт.
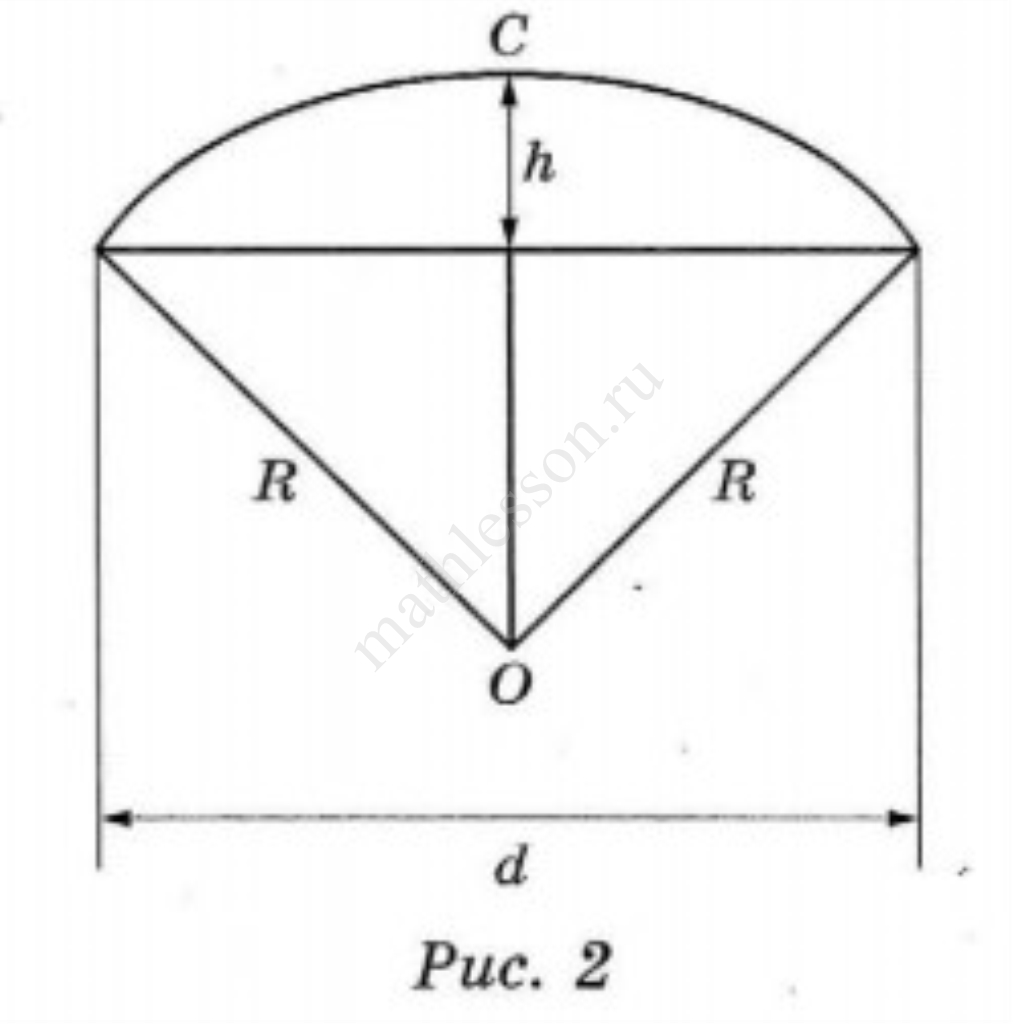
Оля и Аня сумели измерить расстояние между концами соседних спиц $$a$$. Оно оказалось равно $$28$$ см. Высота купола зонта $$h$$ (рис. 2) оказалась равна $$27$$ см, а расстояние $$d$$ между концами спин, образующих дугу окружности, проходящей через вершину зонта, — ровно $$108$$ см.
- Длина зонта в сложенном виде равна $$27$$ см и складывается из длины ручки (рис. 3) и трети длины спицы (зонт в три сложения). Найдите длину спицы, если длина ручки зонта равна $$6,8$$ см.
- Поскольку зонт сшит из треугольников, рассуждала Оля, площадь его поверхности можно найти как сумму площадей треугольников. Вычислите площадь поверхности зонта методом Оли, если высота каждого равнобедренного треугольника, проведённая к основанию, равна $$59$$ см. Ответ дайте в квадратных сантиметрах с округлением до десятков.
- Аня предположила, что купол зонта имеет форму сферического сегмента. Вычислите радиус $$R$$ сферы купола, зная, что $$OC = R$$ (рис. 2). Ответ дайте в сантиметрах.
- Аня нашла площадь купола зонта как площадь поверхности сферического сегмента по формуле $$S = 2\pi Rh$$, где R — радиус сферы, a h — высота сегмента. Рассчитайте площадь поверхности купола способом Ани. Число $$\pi$$ округлите до $$3,14$$. Ответ дайте в квадратных сантиметрах с округлением до целого.
- Рулон ткани имеет длину $$20$$ м и ширину $$90$$ см. На фабрике из этого рулона были вырезаны треугольные клинья для $$15$$ зонтов, таких же, как зонт, который был у Оли и Ани. Каждый треугольник с учётом припуска на швы имеет площадь $$850$$ кв. см. Оставшаяся ткань пошла в обрезки. Сколько процентов ткани рулона пошло в обрезки?
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
1) Длина $$\frac{1}{3}$$ спицы: $$27-6,8=20,2$$ см. Тогда длина всей спицы: $$3\cdot 20,2=60,6$$ см.
2) Площадь одного треугольника: $$S_1=\frac{1}{2}\cdot 28\cdot 59=826$$. Тогда площадь поверхности зонта: $$S_2=12\cdot 826=9912\approx 9910$$ см$$^2$$.
3) Пусть $$OM=x$$; из $$\triangle OLN: OM$$ - высота и медиана $$\to MN=\frac{d}{2}=54$$ см. Из $$\triangle OMN: OM^2+MN^2=ON^2\to x^2+54^2=(x+27)^2\leftrightarrow 54^2=54x+27^2\leftrightarrow$$ $$\leftrightarrow 54x=2916-729\to x=40,5\to R=40,5+27=67,5$$ см.
4) $$S=2\cdot 3,14\cdot 67,5\cdot 27=11445,3\approx 11445$$ см$$^2$$.
5) Количество клиньев: $$15\cdot 12=180$$ шт. Площадь клиньев: $$\frac{180\cdot 850}{100\cdot 100}=15,3$$ м$$^2$$. Площадь рулона: $$20\cdot 0,9=18$$ м$$^2$$. Обрезков: $$18-15,3=2,7$$ м$$^2$$. В процентах $$\frac{2,7}{18}\cdot 100=15%$$
Задание 8
Найдите значение выражения $$\frac{(b^4)^3 \cdot b^8}{b^{21}}$$ при $$b = 5$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 11
На рисунках изображены графики функций вида $$y = ax^2 + bx + c$$. Установите соответствие между знаками коэффициентов $$a$$ и $$c$$ и графиками функций.
Коэффициенты:
А) $$a > 0$$, $$c < 0$$
Б) $$a > 0$$, $$c > 0$$
В) $$a < 0$$, $$c > 0$$
ГРАФИКИ
В таблице под каждой буквой укажите соответствующий номер.
| А | Б | В |
Задание 12
Перевести значение температуры по шкале Фаренгейта в шкалу Цельсия позволяет формула $$t_C = \frac{5}{9}(t_F - 32)$$, где $$t_C$$ — температура в градусах Цельсия, $$t_F$$ — температура в градусах Фаренгейта. Скольким градусам по шкале Цельсия соответствует $$5$$ градусов по шкале Фаренгейта?
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
$$t_c=\frac{5}{9}(5-32)=-15$$
Задание 14
В кафе есть только квадратные столики, за каждый из которых могут сесть $$4$$ человека. Если сдвинуть два квадратных столика, то получится стол, за который могут сесть $$6$$ человек. На рисунке изображён случай, когда сдвинули $$3$$ квадратных столика вдоль одной линии. В этом случае получился стол, за который могут сесть $$8$$ человек. Сколько человек может сесть за стол, который получится, если сдвинуть $$22$$ квадратных столика вдоль одной линии?
Задание 15
Один из острых углов прямоугольного треугольника равен $$23^\circ$$. Найдите его другой острый угол. Ответ дайте в градусах.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Сумма острых углов прямоугольного треугольника составляет 90 градусов, тогда второй острый: $$90^{\circ}-23^{\circ}=67^{\circ}$$
Задание 19
Какое из следующих утверждений верно?
- Вписанный угол, опирающийся на диаметр окружности, прямой.
- Если три угла одного треугольника равны соответственно трём углам другого треугольника, то такие треугольники равны.
- Отношение площадей подобных треугольников равно коэффициенту подобия.
В ответ запишите номер выбранного утверждения.
Задание 20
Сократите дробь: $$\frac{48^n}{4^{2n - 1} \cdot 3^{n - 3}}$$
1) Разложим числа:
$$48=2^4\cdot 3,\quad 4=2^2$$
Тогда: $$48^n=(2^4\cdot 3)^n=2^{4n}\cdot 3^{n}$$ и $$4^{2n-1}=(2^2)^{2n-1}=2^{4n-2}$$
2) Подставим в дробь: $$\frac{48^n}{4^{2n-1}\cdot 3^{n-3}} =$$$$\frac{2^{4n}\cdot 3^{n}}{2^{4n-2}\cdot 3^{n-3}}$$
3) Сократим: $$2^{4n-(4n-2)}\cdot 3^{n-(n-3)} =2^{2}\cdot 3^{3} =$$$$4\cdot 27=108$$