Задание 909
Задание 3241
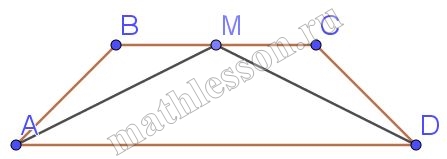
Биссектрисы углов $$A$$ и $$D$$ параллелограмма $$ABCD$$ пересекаются в точке $$M$$, лежащей на стороне $$BC$$. Докажите, что $$M$$ — середина $$BC$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


1) $$\angle A=\angle D\Rightarrow$$ $$\angle BAM=\angle MDC$$
2) $$\angle BAM=\angle MAD$$(AM-биссектриса ); $$\angle MAD=\angle BMA$$(накрест лежащие) $$\Rightarrow \angle BAM=\angle BMA\Rightarrow$$ $$\Delta ABM$$ - равнобедренный
3)Аналогично $$\Delta MCD$$ - равнобедренный $$\Rightarrow$$ $$AB=BM; MC=CD$$, но $$AB=CD\Rightarrow BM=MO$$
Задание 1837
Биссектрисы углов $$A$$ и $$D$$ параллелограмма пересекаются в точке $$E$$ стороны $$BC$$. Докажите, что $$BE=EC$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 740
Биссектрисы углов $$C$$ и $$D$$ параллелограмма $$ABCD$$ пересекаются в точке $$L$$, лежащей на стороне $$AB$$. Докажите, что $$L$$ — середина $$AB$$.
Задание 757
Биссектрисы углов $$A$$ и $$D$$ параллелограмма $$ABCD$$ пересекаются в точке $$K$$, лежащей на стороне $$BC$$. Докажите, что $$K$$ — середина $$BC$$.
Задание 1451
Биссектрисы углов $$B$$ и $$C$$ параллелограмма $$ABCD$$ пересекаются в точке $$T$$, лежащей на стороне $$AD$$. Докажите, что $$T$$ — середина $$AD$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!