ОГЭ 2024. Вариант 3 Ященко 36 вариантов ФИПИ школе.
Решаем 3 вариант ОГЭ Ященко 2024 года сборника ФИПИ школе 36 вариантов. Полный разбор всего 3 варианта (всех заданий) Ященко 2024 ФИПИ 36 вариантов.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 1-5
План местности
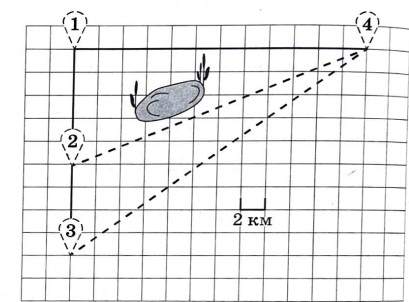
Гриша летом отдыхает у дедушки в деревне Грушёвка. В пятницу они собираются съездить на велосипедах в село Абрамово на ярмарку. Из деревни Грушёвка в село Абрамово можно проехать по прямой лесной дорожке. Есть более длинный путь: по прямолинейному шоссе через деревню Таловка до деревни Новая, где нужно повернуть под прямым углом направо на другое шоссе, ведущее в село Абрамово. Есть и третий маршрут: в деревне Таловка можно свернуть на прямую тропинку в село Абрамово, которая идёт мимо озера.
Лесная дорожка и тропинка образуют с шоссе прямоугольные треугольники. По шоссе Гриша с дедушкой едут со скоростью 15 км/ч, а по лесной дорожке и тропинке - со скоростью 12 км/ч. На плане изображено взаимное расположение населённых пунктов, длина стороны каждой клетки равна 2 км.
1. Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты. Заполните таблицу, в бланк ответов перенесите последовательность трёх цифр без пробелов, запятых и других дополнительных символов.
| Насел. пункты | д. Новая | с. Абрамово | д. Таловка |
| Цифры |
2. Сколько километров проедут Гриша с дедушкой от деревни Грушёвка до села Абрамово, если они поедут по шоссе через деревню Новая?
3. Найдите расстояние от деревни Таловка до села Абрамово по прямой. Ответ дайте в километрах. Ответ:
4. Сколько минут затратят на дорогу из деревни Грушёвка в село Абрамово Гриша с дедушкой, если они поедут сначала по шоссе, а затем свернут в Таловке на прямую тропинку, которая проходит мимо озера? Ответ:
5. В таблице указана стоимость (в рублях) некоторых продуктов в четырёх магазинах, расположенных в деревне Грушёвка, селе Абрамово, деревне Таловка и деревне Новая.
| Наименование продукта | д. Грушёвка | с. Абрамово | д. Таловка | д. Новая |
| Молоко (1 л) | 75 | 77 | 70 | 80 |
| Хлеб (1 батон) | 40 | 35 | 43 | 45 |
| Сыр «Российский» (1 кг) | 560 | 540 | 580 | 520 |
| Говядина (1 кг) | 560 | 530 | 540 | 590 |
| Картофель (1 кг) | 30 | 45 | 42 | 35 |
Гриша с дедушкой хотят купить 4 л молока, 5 батонов хлеба и 2 кг говядины. В каком магазине такой набор продуктов будет стоить дешевле всего? В ответ запишите стоимость данного набора в этом магазине.
Задание 12
Энергия заряженного конденсатора $$W$$ (в Дж) вычисляется по формуле $$W = \frac{q^2}{2C}$$, где $$C$$ — ёмкость конденсатора (в Ф), а $$q$$ — заряд на одной обкладке конденсатора (в Кл). Найдите энергию конденсатора (в Дж) ёмкостью $$10^{-4}$$ Ф, если заряд на его обкладке равен $$0,0018$$ Кл.
Задание 19
Какие из следующих утверждений верны?
- Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.
- Если диагонали параллелограмма равны, то этот параллелограмм является ромбом.
- Расстояние от точки, лежащей на окружности, до центра окружности равно радиусу.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Задание 20
Решите систему уравнений: $$ \left\{\begin{aligned} 5x^2 - 11x = y \\ 5x - 11 = y \end{aligned}\right. $$
1) Приравниваем правые части: $$5x^2 - 11x = 5x - 11.$$ Переносим всё в одну сторону: $$5x^2 - 16x + 11 = 0.$$ Находим дискриминант: $$D = (-16)^2 - 4\cdot 5\cdot 11 = 256 - 220 = 36.$$ Корни: $$x_{1,2} = \dfrac{16 \pm \sqrt{36}}{2\cdot 5} = \dfrac{16 \pm 6}{10}.$$ Тогда $$x_1 = \dfrac{16 - 6}{10} = 1,\qquad x_2 = \dfrac{16 + 6}{10} = \dfrac{22}{10} = \dfrac{11}{5}.$$
2) Находим значения $$y$$ по второму уравнению.
Для $$x = 1$$: $$y = 5\cdot 1 - 11 = -6.$$ Для $$x = \dfrac{11}{5}$$: $$y = 5\cdot \dfrac{11}{5} - 11 = 11 - 11 = 0.$$ Решения: $$(1;-6),\ \left(\dfrac{11}{5};0\right).$$