Задание 352
Задание 2592
Окружности с центрами в точках $$E$$ и $$F$$ пересекаются в точках $$C$$ и $$D$$, причём точки $$E$$ и $$F$$ лежат по одну сторону от прямой $$CD$$. Докажите, что $$CD\perp EF$$ .
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


1) Пусть $$CD\cup EF=M$$; $$EC=ED$$ (радиусы) $$\Rightarrow$$ $$\bigtriangleup ECD$$ - равнобедренный. $$CF=FD$$ (радиусы) $$\Rightarrow$$ $$\bigtriangleup CFD$$ - равнобедренный
2) из 1 и общий $$EF$$ $$\bigtriangleup ECF=\bigtriangleup EDF$$ $$\Rightarrow$$ $$\angle CFE=\angle DFE$$ $$\Rightarrow$$ $$FM$$ - бисекрисса, но тогда она и высота $$\Rightarrow$$ $$CD\perp EF$$
Задание 926
Окружности с центрами в точках $$P$$ и $$Q$$ пересекаются в точках $$K$$ и $$L$$, причём точки $$P$$ и $$Q$$ лежат по одну сторону от прямой $$KL$$. Докажите, что $$PQ\perp KL$$ .
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 638
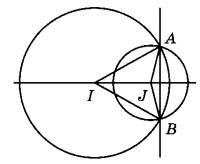
Окружности с центрами в точках $$I$$ и $$J$$ пересекаются в точках $$A$$ и $$B$$, причём точки $$I$$ и $$J$$ лежат по одну сторону от прямой $$AB$$. Докажите, что отрезки $$AB$$ и $$AJ$$ перпендикулярны.
Точка I равноудалена от точек A и B, поэтому эта точка лежит на серединном перпендикуляре к отрезку AB. Аналогично, точка J лежит на серединном перпендикуляре к отрезку AB. Значит, прямая, содержащая точки I и J, является серединным перпендикуляром к отрезку AB. Следовательно, прямые IJ и АВ перпендикулярны.