Задание 1765
Задание 1765
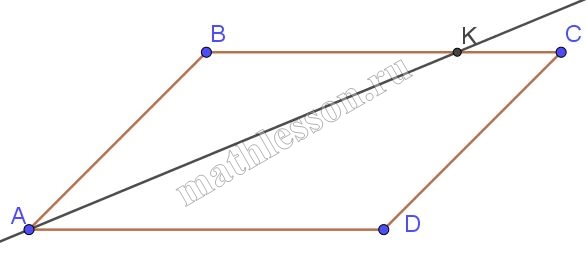
Биссектриса угла $$A$$ параллелограмма $$ABCD$$ пересекает сторону $$BC$$ в точке $$K$$. Найдите периметр параллелограмма, если $$BK=8$$, $$CK=13$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Аналоги к этому заданию:
Задание 4907
Биссектриса угла $$A$$ параллелограмма $$ABCD$$ пересекает сторону $$BC$$ в точке $$K$$. Найдите периметр параллелограмма, если $$BK=7$$, $$CK=12$$.
$$\angle BAK=\angle KAD$$(свойство биссеткрисы), $$\angle BKA=\angle KAD$$ (накрестлежащие углы), следовательно, $$\angle BAK=\angle BKA$$, тогда треугольник ABK - равнобедренный и AB=BK=7, но BC=BK+KC=7+132=19=AD, тогда периметр составит: $$2*(7+19)=52$$
Задание 3870
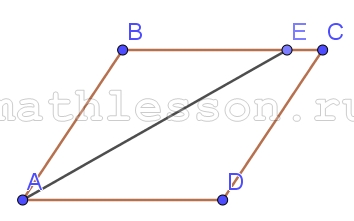
Биссектриса угла $$A$$ параллелограмма $$ABCD$$ пересекает сторону $$BC$$ в точке $$E$$. Найдите периметр параллелограмма, если $$BE=5$$, $$CE=14$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
$$BC=5+14=19=AO$$; $$\angle BAE=\angle EAD$$ (биссектриса); $$\angle EAD=\angle BEA$$ (накрестлежащие) $$\Rightarrow$$ $$AB=BE=5=CD$$; $$P=(19+5)\cdot2=48$$
Задание 4100
Биссектриса угла $$A$$ параллелограмма $$ABCD$$ пересекает сторону $$BC$$ в точке $$M$$. Найдите периметр параллелограмма, если $$BM=12$$, $$CM=15$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
$$BC=AD=12+15=27$$; $$\angle MAD=\angle AMB$$ (накрестлежащие); $$\angle BAM=\angle MAD$$ (биссектриса) $$\Rightarrow$$ $$\bigtriangleup ABM$$ - равнобедренный $$\Rightarrow$$ $$AB=BM=12$$; $$P_{ABCD}=12\cdot2+27\cdot2=24+54=78$$
Задание 4159
Биссектриса угла $$A$$ параллелограмма $$ABCD$$ пересекает сторону $$BC$$ в точке $$E$$. Найдите периметр параллелограмма, если $$BK=12$$, $$CK=5$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
$$BC=12+5=17=AD$$
$$\angle BAE=\angle EAD$$ - биссектриса
$$\angle EAD=\angle BEA$$ - (накрестлежащие)
$$\Rightarrow$$ $$\angle BAE=\angle BEA$$ $$\Rightarrow$$
$$AB=BE=12=CD$$
$$P=2AB+2BC=2\cdot12+2\cdot17=24+34=58$$
Задание 4262
Биссектриса угла $$A$$ параллелограмма $$ABCD$$ пересекает сторону $$BC$$ в точке $$K$$. Найдите периметр параллелограмма, если $$BK=4$$, $$CK=18$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 3009
Биссектриса угла $$A$$ параллелограмма $$ABCD$$ пересекает сторону $$BC$$ в точке $$K$$. Найдите периметр параллелограмма, если $$BK=10$$, $$CK=3$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
1) $$BC=BK+KC=13$$
2) $$\angle BAK=\angle KAD$$(AK-биссектриса ); $$\angle KAD=\angle AKB$$ (накрест лежащие )$$\Rightarrow$$ $$\angle BAK=\angle BKA$$$$\Rightarrow$$ $$AB=BK=10$$
3) $$P_{ABCD}=(13+10)*2=52$$
Задание 3077
Биссектриса угла $$A$$ параллелограмма $$ABCD$$ пересекает сторону $$BC$$ в точке $$K$$. Найдите периметр параллелограмма, если $$BK=10$$, $$CK=7$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
1) $$BC=AD=10+7=17$$
2) $$\angle BAE=\angle EAD$$ ( AE - биссектриса ); $$\angle EAD=BEA$$ (накрест лежащие) $$\Rightarrow$$ $$\angle BEA=\angle BAE\Rightarrow$$ $$AB=BE=10=CD$$
3) $$P_{ABCD}=(17+10)*2=54$$
Задание 3224
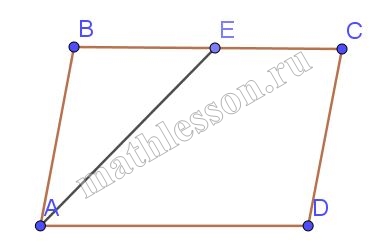
Биссектриса угла $$A$$ параллелограмма $$ABCD$$ пересекает сторону $$BC$$ в точке $$E$$. Найдите периметр параллелограмма, если $$BE=5$$, $$CE=16$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
- $$BC=5+16=21=AD $$
- $$\angle BAE=\angle EAD$$(AE-биссектриса )
- $$\angle BEA=\angle EAD$$(накрест лежащие ), тогда $$BE=AB=5=CD $$
- $$P=2(5+21)=52$$
Задание 935
Биссектриса угла $$A$$ параллелограмма $$ABCD$$ пересекает сторону $$BC$$ в точке $$K$$. Найдите периметр параллелограмма, если $$BK=10$$, $$CK=18$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 331
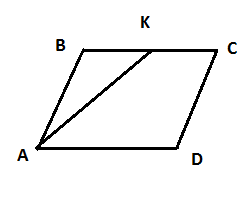
Биссектриса угла $$A$$ параллелограмма $$ABCD$$ пересекает сторону $$BC$$ в точке $$K$$. Найдите периметр параллелограмма, если $$BK=11$$, $$CK=20$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!