Четырёхугольники
Задание 1231
Биссектрисы углов $$A$$ и $$B$$ параллелограмма $$ABCD$$ пересекаются в точке $$K$$. Найдите площадь параллелограмма, если $$BC=6$$, а расстояние от точки $$K$$ до стороны $$AB$$ равно $$6$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 1550
Боковые стороны $$AB$$ и $$CD$$ трапеции $$ABCD$$ равны соответственно $$24$$ и $$25$$, а основание $$BC$$ равно $$9$$. Биссектриса угла $$ADC$$ проходит через середину стороны $$AB$$. Найдите площадь трапеции.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 4211
В выпуклом равностороннем шестиугольнике $$ABCDEF$$ углы при вершинах $$A$$, $$C$$ и $$E$$ – прямые. Найдите площадь шестиугольника, если его сторона равна $$3\sqrt{3-\sqrt{3}}$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 330
В выпуклом четырёхугольнике $$ABCD$$ диагонали пересекаются в точке $$O$$. Точка $$N$$ принадлежит отрезку $$AC$$. Известно, что $$BO=15$$, $$DO=9$$, $$AC=30$$. Найдите $$CN$$, если площадь треугольника $$ABN$$ в $$7,5$$ раза меньше площади четырёхугольника $$ABCD$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 3263
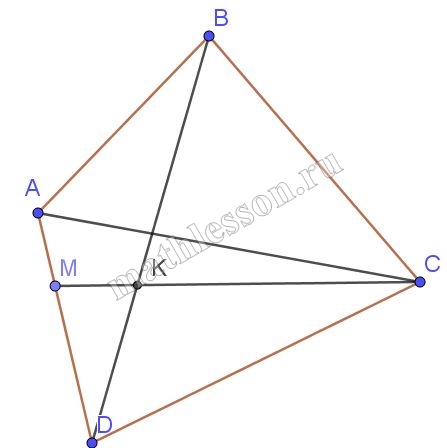
В выпуклом четырехугольнике $$ABCD$$ отрезок $$CM$$, соединяющий вершину $$C$$ с точкой $$M$$, расположенной на стороне $$AD$$, пересекает диагональ $$BD$$ в точке $$K$$. Известно, что $$CK:KM=2:1$$, $$CD:DK=5:3$$ и $$\angle ABD+\angle ACD=180^{\circ}$$. Найдите отношение стороны $$AB$$ и диагонали $$AC$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


1) Пусть $$\angle ADB =\alpha$$ , $$\angle ADC=\beta$$
по т. Синусов : $$\Delta ABD$$: $$\frac{AB}{\sin \alpha }=\frac{AD}{\sin \angle ABD}(1)$$
$$\sin \angle BAD=$$$$\sin(180-\angle ACD)=$$$$\sin \angle ACD(2)$$
$$\Delta ACD$$ : $$\frac{AD}{\sin \angle ACD}=$$$$\frac{AC}{\sin \beta }(3)$$
Учитывая (1) и (2) и (3) : $$\frac{AB}{\sin \alpha }=\frac{AC}{\sin \beta }\Leftrightarrow$$ $$\frac{AB}{AC}=\frac{\sin\alpha }{\sin \beta }$$
2) Пусть $$MK=x$$ $$\Rightarrow$$ $$CK=2x$$, $$CM=3x$$, $$CD=5y$$ $$\Rightarrow$$ $$DK=3y$$, $$\angle CMD=\delta$$
Из $$\Delta MDK$$ : $$\frac{x}{\sin \alpha }=\frac{3y}{\sin \delta }\Rightarrow$$ $$\sin \alpha =\frac{x\sin \delta }{3y}$$
Из $$\Delta MDC$$ : $$\frac{3x}{\sin \beta }=\frac{5y}{\sin \delta }\Rightarrow$$ $$\sin \beta =\frac{3x \sin \delta }{5y}$$
Тогда $$\frac{AB}{AC}=\frac{\sin \alpha }{\sin \beta }=$$$$\frac{x \sin \delta }{3y}*\frac{5y}{3x \sin \delta }=$$$$\frac{5}{9}$$
Задание 3931
В выпуклом четырёхугольнике $$ABCD$$ точка $$E$$ – точка пересечения диагоналей. Известно, что площадь каждого из треугольников $$ABE$$ и $$DCE$$ равна $$1$$, площадь четырёхугольника $$ABCD$$ не превосходит $$4$$, $$AD=3$$. Найдите длину стороны $$BC$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


1) $$S_{ABC}=S_{CED}=1$$ $$\Rightarrow$$ $$BE\cdot AE=CE\cdot ED$$ $$\Rightarrow$$ $$\frac{BE}{ED}=\frac{CE}{EA}$$; $$\angle BEC=\angle AED$$ $$\Rightarrow$$ $$\bigtriangleup BEC\sim\bigtriangleup AED$$ $$\Rightarrow$$ дана трапеция.
2) Пусть НМ - высота $$\Rightarrow$$ $$S_{BEC}=\frac{1}{2}BC\cdot HE$$; $$S_{AED}=\frac{1}{2}EM\cdot AD$$. Пусть $$EM=x$$ $$\Rightarrow$$ $$HE=kx$$, где $$k$$ - коэфф. подобия $$\Rightarrow$$ $$BC=k\cdot3$$ $$\Rightarrow$$
$$S_{BEC}+S_{AED}=\frac{1}{2}\cdot3k\cdot kx+\frac{1}{2}\cdot3x=\frac{1}{2}\cdot3x(k^{2}+1)\leq2$$ $$\Rightarrow$$ $$x(k^{2}+1)\leq\frac{4}{3}$$ $$(1)$$
$$S_{ABCD}=\frac{3k+3}{2}\cdot(kx+x)<4$$ $$\Rightarrow$$ $$x(k+1)^{2}\leq\frac{8}{3}$$ $$(2)$$
Поделим первое на второе: $$\frac{k^{2}+1}{(k+1)^{2}}\leq\frac{4}{3}\cdot\frac{3}{8}$$ $$\Leftrightarrow$$ $$\frac{k^{2}+1}{(k+1)^{2}}\leq\frac{1}{2}$$ $$\Leftrightarrow$$ $$2k^{2}+2\leq k^{2}+2k+1$$ $$\Leftrightarrow$$ $$k^{2}-2k+1\leq0$$ $$\Leftrightarrow$$ $$(k-1)^{2}\leq0$$ $$\Leftrightarrow$$ $$k=1$$ $$\Rightarrow$$ $$BC=1\cdot3=3$$
Задание 1920
В параллелограмме $$ABCD$$ проведена диагональ $$AC$$. Точка $$O$$ является центром окружности, вписанной в треугольник $$ABC$$. Расстояния от точки $$O$$ до точки $$A$$ и прямых $$AD$$ и $$AC$$ соответственно равны $$25$$, $$13$$ и $$7$$. Найдите площадь параллелограмма $$ABCD$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 2554
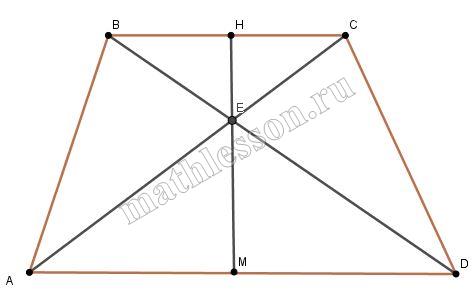
В равнобедренной трапеции $$ABCD$$ боковые стороны равны меньшему основанию $$BC$$. К диагоналям трапеции провели перпендикуляры $$BH$$ и $$CE$$. Найдите площадь четырёхугольника $$BCEH$$, если площадь трапеции равна $$36$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 3358
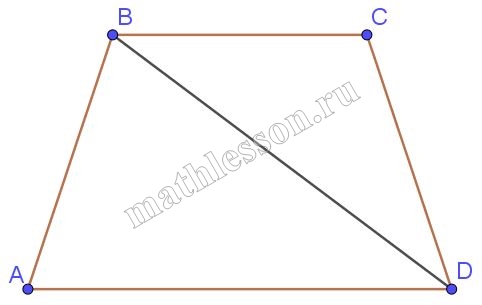
В равнобедренной трапеции $$ABCD$$ длина боковой стороны $$AB$$ равна $$2$$ и длина меньшего основания $$BC$$ равна $$2$$. Найдите площадь трапеции, если $$BD\perp AB$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


1) Пусть $$\angle DBC=\alpha$$ , тогда т.к. BC=CD, $$\angle BCD=\alpha$$, $$\angle C=180-2\alpha$$
2) По свойству углов трапеции $$\angle C+\angle D=180\Rightarrow$$ $$\angle D=180-(180-2\alpha )=2\alpha$$ $$\Rightarrow \angle BDA=\alpha$$
3) Пусть BD=y. Тогда из $$\Delta BCD$$:
$$CD^{2}=BC^{2}+AD^{2}-2BC*AD*\cos CBD$$
$$2^{2}=2^{2}+y^{2}-2*2*y*\cos \alpha \Leftrightarrow$$ $$y^{2}-4y*\cos \alpha =0$$
$$y(y-4\cos\alpha )=0$$, т.к. y-длина, то $$y\neq 0$$, тогда $$y-4\cos \alpha =0\Rightarrow y=4\cos\alpha$$
4) Из $$\Delta ABD$$:
$$\frac{AB}{BD}=tgBDA\Rightarrow$$ $$\frac{2}{4\cos\alpha }=tg\alpha =\frac{\sin\alpha }{\cos\alpha }\Leftrightarrow$$ $$\sin\alpha =\frac{1}{2}\Rightarrow$$ $$\alpha =30\Rightarrow$$ $$y=4*\frac{\sqrt{3}}{2}=2\sqrt{3}$$
5) $$S_{ABCD}=S_{BCD}+S_{ABD}=$$$$\frac{1}{2}*BC*BD*\sin CBD+\frac{1}{2}*AB*BD=$$$$\frac{1}{2}*2*2\sqrt{3}*\frac{1}{2}+\frac{1}{2}*2*2\sqrt{3}=$$$$\sqrt{3}+2\sqrt{3}=3\sqrt{3}$$
Задание 3380
В равнобедренной трапеции $$ABCD$$ углы при основании $$AD$$ равны $$30$$, диагональ $$AC$$ является биссектрисой угла $$BAD$$. Биссектриса угла $$BCD$$ пересекает основание $$AD$$ в точке $$M$$, а отрезок $$BM$$ пересекает диагональ $$AC$$ в точке $$K$$. Найдите площадь треугольника $$AKM$$, если площадь трапеции $$ABCD$$ равна $$2+\sqrt{3}$$ см2.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


1) Пусть $$AB=CD=a$$, $$\angle BAC=\angle CAD$$(AC-биссектриса ), $$\angle CAD=\angle ACB$$(накрест лежащие),тогда $$\angle BAC=\angle BCA\Rightarrow$$ $$AB=BC=a$$
2) Аналогично для $$\Delta CMD$$ : $$\angle BCM=\angle CMD$$, $$\angle BCM=\angle MCD$$, тогда $$\angle CMD=\angle MCD$$ и $$CD=MD=a$$
3) из п.2 и параллельности BC и MD получим, что BCDM-параллелограмм; $$BM=CD=a$$, $$\Delta A_{1}BM$$ -равнобедренный; $$\angle ABM=180-2*30=120$$
По теореме косинусов : $$AM=\sqrt{AB^{2}+BM^{2}-2AB*BM*\cos ABM}=$$$$\sqrt{a^{2}+a^{2}-2*a*a*\cos 120}=a\sqrt{3}$$
4) AK-биссектриса , тогда $$\frac{AB}{AM}=\frac{AK}{KM}=$$$$\frac{a}{\sqrt{30}}=\frac{1}{\sqrt{3}}$$, тогда $$\frac{KM}{BM}=\frac{\sqrt{3}}{\sqrt{3}+1}$$ и $$S_{\Delta AKM}=\frac{\sqrt{3}}{\sqrt{3}+1}S_{ABM}$$
5) Пусть $$CN\perp AD$$,тогда из $$\Delta CND$$: $$CH=CD*\sin D=\frac{a}{2}$$
6) $$S_{ABD}=\frac{a+a+a\sqrt{3}}{2}*\frac{a}{2}=$$$$\frac{a^{2}}{4}(2+\sqrt{3})=2+\sqrt{3}\Rightarrow$$ $$a^{2}=4\Rightarrow a=2$$
7)$$S_{ABM}=\frac{1}{2}*a*a* \sin 120=$$$$\frac{\sqrt{3}a^{2}}{4}=\sqrt{3}$$
$$S_{AKM}=\frac{\sqrt{3}}{\sqrt{3}+1}*\sqrt{3}=$$$$\frac{3}{\sqrt{3}+1}$$
Задание 4439
В трапеции $$ABCD$$ на продолжении основания $$BC$$ взята точка $$M$$ таким образом, что прямая $$AM$$ отсекает от трапеции $$ABCD$$ треугольник, площадь которого в $$4$$ раза меньше площади трапеции $$ABCD$$. Найдите длину отрезка $$CM$$, если $$AD=8$$, $$BC=4$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Решение временно отсутствует, можете найти его в моем видео-разборе ( вначале варианта )
Задание 4171
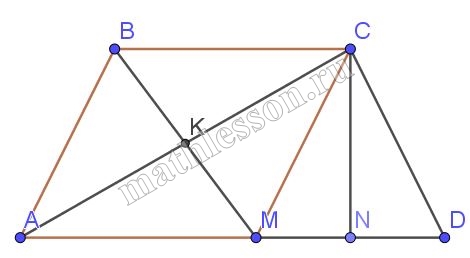
В трапеции $$ABCD$$ основания $$AD$$ и $$BC$$ равны $$6$$ см и $$10$$ см соответственно. На продолжении $$BC$$ выбрана такая точка $$M$$, что прямая $$AM$$ отсекает от площади трапеции $$\frac{1}{4}$$ её часть. Найдите длину отрезка CM.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


1) Пусть $$AH=h$$ - высота
$$S_{ABCD}=\frac{BC+AD}{2}\cdot AH=\frac{6+10}{2}\cdot h=h$$
тогда $$S_{AKD}=\frac{1}{2}AD\cdot x$$, х - высота
$$S_{AKD}=KM$$
$$S_{AKD}=\frac{1}{2}\cdot6\cdot x=3x=\frac{1}{4}S_{ABCD}=2h$$
$$x=\frac{2h}{3}$$
2) $$LK+KM=h$$ $$\Rightarrow$$ $$LK=\frac{h}{3}$$ - высота $$\bigtriangleup CMK$$
3) $$\bigtriangleup AKD\sim\bigtriangleup CMK$$ по трем углам $$\Rightarrow$$
$$\frac{AD}{CM}=\frac{KM}{KL}=\frac{2h}{3}\div\frac{h}{3}=\frac{2}{1}$$
$$CM=\frac{1}{2}AD=\frac{1}{2}\cdot6=3$$
Задание 3191
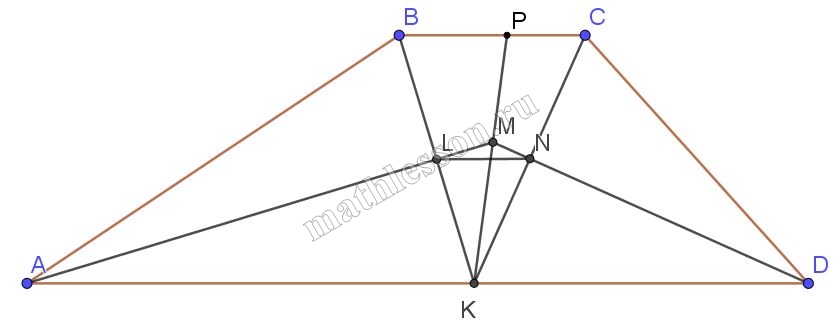
В трапеции $$ABCD$$ с боковыми сторонами $$AB=9$$ и $$CD=5$$ биссектриса угла $$D$$ пересекает биссектрисы углов $$A$$ и $$C$$ в точках $$M$$ и $$N$$ соответственно, а биссектриса угла $$B$$ пересекает те же две биссектрисы в точках $$L$$ и $$K$$, причём точка $$K$$ лежит на основании $$AD$$. Найдите отношение $$MN:KL$$, если $$LM:KN=3:7$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


1) $$\angle ABK=\angle CBK$$ (BL-биссектриса ), $$\angle CBK=\angle AKB$$ (накрест лежащие) $$\Rightarrow AB=AK=9$$; AL-биссектриса , медиана и высота равнобедренного $$\Delta ABK$$: $$AL\perp BK$$ и $$BL\perp LK(1)$$
2) Аналогично из $$\Delta CDK$$ : $$CD=DK=5$$; $$DN\perp CK$$; $$CN=NK$$. С учетом (1) - LN-средняя линия $$\Delta BKC$$ и AD=14
3) $$MK\cap LN=Q$$; $$KM\cap BC=P$$. Тогда : $$LN\left | \right |BC$$, $$BC\left | \right |AD\Rightarrow$$ $$LN\left | \right |AD$$ и : $$\Delta LMN\sim \Delta AMD\Rightarrow$$ $$QN:QL=KD:KA=5:9\Rightarrow$$ $$QL=\frac{9 QN}{5}(2)$$
4) $$\angle MLN=\angle MNK=90\Rightarrow$$ около $$MNKL$$ можно описать окружность ($$\angle MLK+\angle MNK=180$$) $$\Rightarrow \Delta LMQ\sim \Delta QNM$$: $$\frac{LM}{NK}=\frac{MQ}{QN}=\frac{3}{7}(3)$$
5) $$\Delta LQK\sim \Delta MQN\Rightarrow$$ $$\frac{MN}{LK}=\frac{MQ}{QL}$$. С учетом (2) : $$\frac{NQ}{QL}=\frac{MQ}{\frac{9QN}{5}}=$$$$\frac{5MQ}{9 QN}(3)$$. С учетом (3): $$\frac{5 MQ}{9 QN}=\frac{5}{9}*\frac{3}{7}=$$$$\frac{5}{21}=\frac{MN}{LK}$$
Задание 1894
В трапеции проведён отрезок, параллельный основаниям и делящий её на две трапеции одинаковой площади. Найдите длину этого отрезка, если основания трапеции равны $$24\sqrt{2}$$ и $$7\sqrt{2}$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 2426
В четырёхугольнике $$ABCD$$ диагонали пересекаются в точке $$O$$ под углом $$\alpha$$. Точка $$F$$ принадлежит отрезку $$AC$$. Известно, что $$BO=10$$, $$DO=14$$, $$AC=18$$. Найдите $$AF$$, если площадь треугольника $$FBC$$ в четыре раза меньше площади четырёхугольника $$ABCD$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!