Задание 4242
Задание 4242
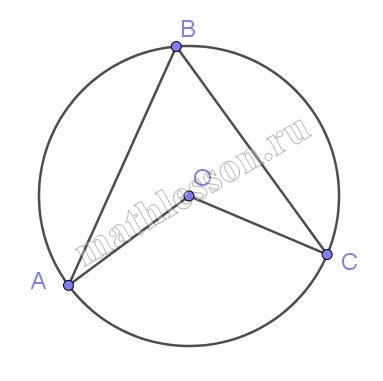
Треугольник $$ABC$$ вписан в окружность с центром в точке $$O$$. Точки $$O$$ и $$C$$ лежат в одной полуплоскости относительно прямой $$AB$$. Найдите угол $$ACB$$, если угол $$AOB$$ равен $$152^\circ$$. Ответ дайте в градусах.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Введем обозначения как показано на рисунке:
Угол AOB - центральный, значит его величина равна величине дуги на которую он опирается, то есть дуга AB = 152. Угол С - вписанный, его величина равна половине величины, на которую он опирается, то есть половину AB: 152/2=76
Аналоги к этому заданию:
Задание 3179
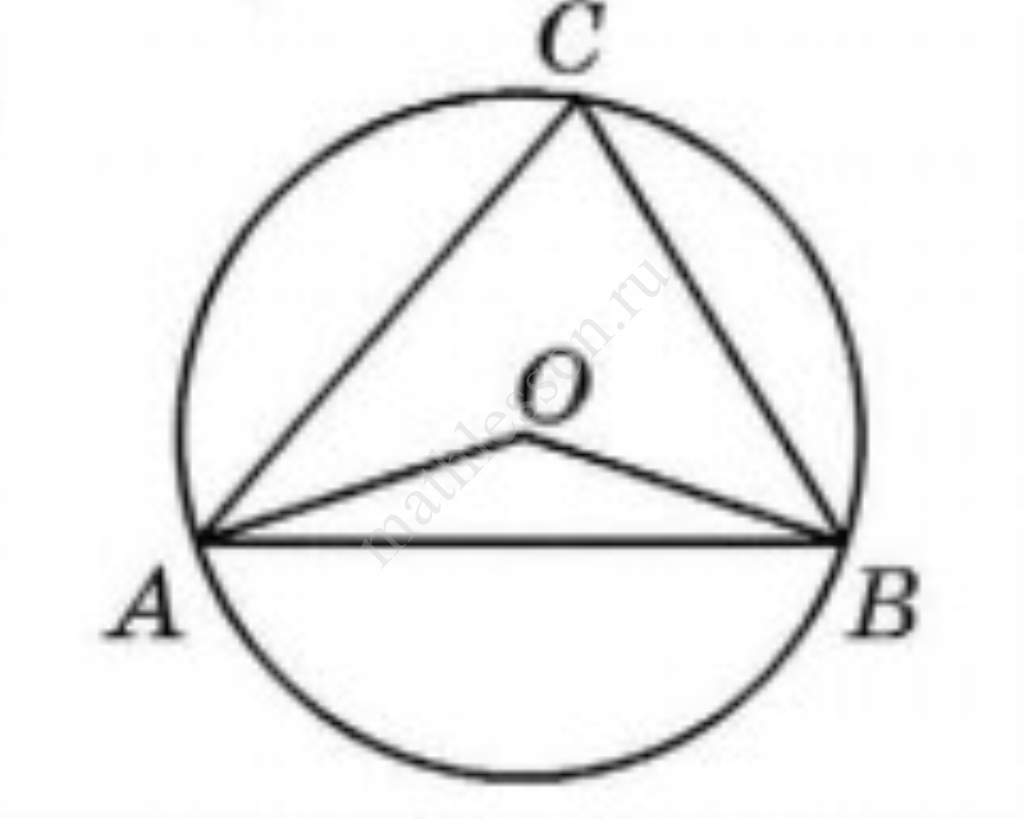
Треугольник $$ABC$$ вписан в окружность с центром в точке $$O$$. Найдите градусную меру угла $$B$$ треугольника $$ABC$$, если угол $$AOC$$ равен $$140^\circ$$. Ответ дайте в градусах.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
$$\angle ABC=\frac{1}{2}\angle AOC$$ (свойство вписанного угла)
$$\angle ABC=\frac{1}{2}*140=70$$
Задание 1703
Треугольник $$ABC$$ вписан в окружность с центром в точке $$O$$. Точки $$O$$ и $$C$$ лежат в одной полуплоскости относительно прямой $$AB$$. Найдите угол $$ACB$$, если угол $$AOB$$ равен $$115^\circ$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 1715
Треугольник $$ABC$$ вписан в окружность с центром в точке $$O$$. Точки $$O$$ и $$C$$ лежат в одной полуплоскости относительно прямой $$AB$$. Найдите угол $$ACB$$, если угол $$AOB$$ равен $$73^\circ$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 2597
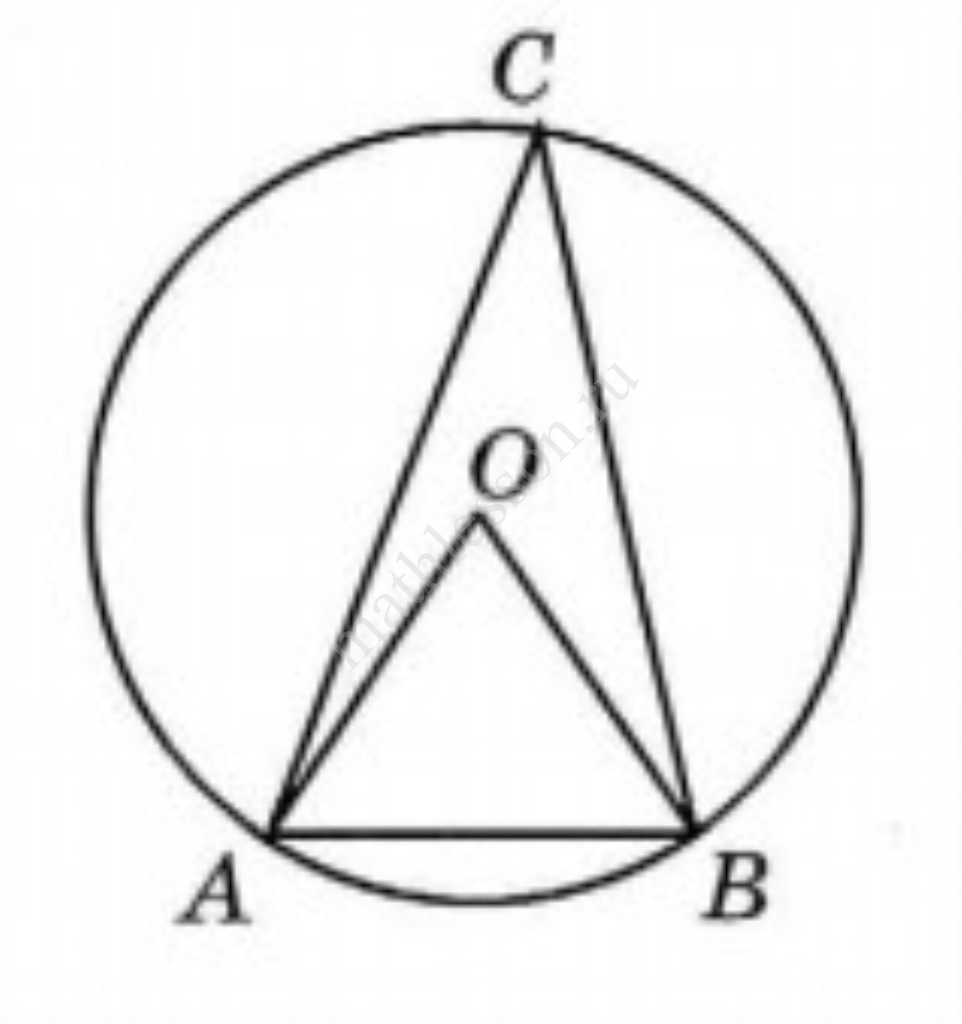
Треугольник $$ABC$$ вписан в окружность с центром в точке $$O$$. Точки $$O$$ и $$C$$ лежат в одной полуплоскости относительно прямой $$AB$$. Найдите градусную меру угла $$ACB$$, если угол $$AOB$$ равен $$167^\circ$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
