ОГЭ 2021. Вариант 9 Ященко 36 вариантов ФИПИ школе.
Решаем 9 вариант ОГЭ Ященко 2021 года сборника ФИПИ школе 36 вариантов. Полный разбор всего 9 варианта (всех заданий).
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 1-5
Шины
Автомобильное колесо, как правило, представляет из себя металлический диск с установленной на него резиновой шиной. Диаметр диска совпадает с диаметром внутреннего отверстия в шине.
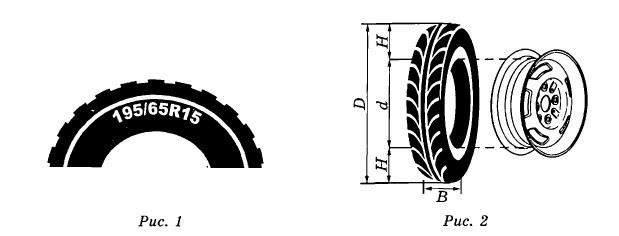
Для маркировки автомобильных шин применяется единая система обозначений. Например, $$195/65 R15$$ (рис. 1). Первое число (число $$195$$ в приведённом примере) обозначает дирину шины в миллиметрах (параметр $$B$$ на рисунке 2). Второе число (число $$65$$ в приведённом примере) - процентное отношение высоты боковины (параметр $$H$$ на рисунке 2) к ширине шины, то есть $$100 \cdot \frac{H}{B}$$.
Последующая буква обозначает тип конструкции шины. В данном примере буква $$R$$ означает, что шина радиальная, то есть нити каркаса в боковине шины расположены вдоль радиусов колеса. На всех легковых автомобилях применяются шины радиальной конструкции.
За обозначением типа конструкции шины идёт число, указывающее диаметр диска колеса $$d$$ в дюймах (в одном дюйме $$25,4$$ мм). Таким образом, общий диаметр колеса $$D$$ легко найти, зная диаметр диска и высоту боковины. Возможны дополнительные маркировки, обозначающие допустимую нагрузку на шину, сезонность использования, тип дорожного покрытия и другие параметры.
Завод производит легковые автомобили определённой модели и устанавливает на них колёса с шинами маркировки $$205/60 R16$$.
1. Завод допускает установку шин с другими маркировками. В таблице показаны разрешённые размеры шин.
| Ширина шины (мм)/Диаметр диска (дюймы) | 15 | 16 | 17 | 18 |
| 195 | 195/65 | 195/60 | 195/55 | не разр. |
| 205 | 205/60 | 205/55, 205/60 | 205/50 | 205/45 |
| 215 | 215/60 | 215/55 | 215/50 | 215/40, 215/45 |
| 225 | не разр. | 225/50 | 225/50, 225/45 | 225/40 |
Какой наименьшей ширины шины можно устанавливать на автомобиль, если диаметр диска равен $$17$$ дюймам? Ответ дайте в миллиметрах.
2. На сколько миллиметров радиус колеса с маркировкой $$195/55 R17$$ больше, чем радиус колеса с маркировкой $$225/45 R17$$?
3. Найдите диаметр $$D$$ колеса автомобиля, выходящего с завода. Ответ дайте в сантиметрах.
4. На сколько миллиметров уменьшится диаметр $$D$$ колеса, если заменить шины, установленные на заводе, шинами с маркировкой $$225/40 R18$$?
5. На сколько процентов уменьшится пробег автомобиля при одном обороте колеса, если заменить шины, установленные на заводе, шинами с маркировкой $$225/40 R18$$? Округлите результат до десятых.
Задание 6
Найдите значение выражения $$3\cdot (\frac{5}{6}+\frac{7}{15})$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 7
Какое из данных чисел принадлежит промежутку $$[5; 6]$$?
1) $$\sqrt{5}$$
2) $$\sqrt{6}$$
3) $$\sqrt{24}$$
4) $$\sqrt{32}$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 8
Найдите значение выражения $$\sqrt{20} \cdot \sqrt{1,8}$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


$$\frac{6}{x+5}=-5$$
$$-5(x+5)=6$$
$$-5x-25=6$$
$$5x=-31$$
$$x=-\frac{31}{5}=-6,2$$
Задание 10
В фирме такси в данный момент свободно $$40$$ машин: $$17$$ чёрных, $$15$$ жёлтых и $$8$$ зелёных. Найдите вероятность того, что к заказчику приедет жёлтое такси.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 12
Площадь треугольника вычисляется по формуле $$S = \frac{1}{2}bc \cdot \sin \alpha$$, где $$b$$ и $$c$$ — две стороны треугольника, а $$\alpha$$ — угол между ними. Пользуясь этой формулой, найдите площадь $$S$$, если $$b = 16$$, $$c = 9$$ и $$\sin \alpha = \frac{1}{3}$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 14
Курс воздушных ванн начинают с $$10$$ минут в первый день и увеличивают время этой процедуры в каждый следующий день на $$5$$ минут. В какой по счёту день продолжительность процедуры достигнет $$1$$ часа $$5$$ минут?
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 15
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 16
Центр окружности, описанной около треугольника $$ABC$$, лежит на стороне $$AB$$. Радиус окружности равен $$20,5$$. Найдите $$BC$$, если $$AC = 9$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 17
Периметр ромба равен $$12$$, а один из углов равен $$30^\circ$$. Найдите площадь ромба.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 19
Какое из следующих утверждений верно?
- Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
- Сумма углов прямоугольного треугольника равна $$90^{\circ}$$ градусам.
- Любая биссектриса равнобедренного треугольника является его медианой.
В ответ запишите номер выбранного утверждения.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 20
Решите неравенство: $$(x - 7)^{2} < \sqrt{11}(x - 7)$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


$$(x-7)^{2}-\sqrt{11}(x-7)<0$$
$$(x-7)(x-7-\sqrt{11})<0$$
Начертим координатную прямую, отметим значения х при которых выражение $$(x-7)(x-7-\sqrt{11})$$ равно нулю и расставим знаки значений, которые принимает данное выражение на полученных промежутках:

Выберем те, в которых выражение принимает отрицательные значения: $$(7; 7+\sqrt{11})$$
Задание 21
Первая труба пропускает на $$16$$ литров воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает первая труба, если резервуар объёмом $$105$$ литров она заполняет на $$4$$ минут дольше, чем вторая труба?
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 22
Постройте график функции $$y = \left\{ \begin{aligned} -x^2 - 2x + 1,&\ x \ge -3 \\ -x - 5,&\ x < -3 \end{aligned} \right.$$ и определите, при каких значениях $$m$$ прямая $$y = m$$ имеет с графиком ровно две общие точки.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 23
В равнобедренной трапеции $$ABCD$$ с большим основанием $$AD$$ биссектриса угла $$A$$ пересекается с биссектрисой угла $$C$$ в точке $$F$$, а также пересекает сторону $$CD$$ в точке $$K$$. Известно, что угол $$AFC$$ равен $$150^{\circ}$$. Найдите $$FK$$, если $$CF=6\sqrt{3}$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 24
Известно, что около четырёхугольника $$ABCD$$ можно описать окружность и что продолжения сторон $$AD$$ и $$BC$$ четырёхугольника пересекаются в точке $$K$$. Докажите, что треугольники $$KAB$$ и $$KCD$$ подобны.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 25
На стороне $$BC$$ остроугольного треугольника $$ABC$$ ($$AB\neq AC$$) как на диаметре построена полуокружность, пересекающая высоту $$AD$$ в точке $$M$$, $$AD=80$$, $$MD=64$$, $$H$$ - точка пересечения высот треугольника $$ABC$$. Найдите $$AH$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!