ОГЭ 2022. Вариант 19 Ященко 36 вариантов ФИПИ школе.
Решаем 19 вариант ОГЭ Ященко 2022 года сборника ФИПИ школе 36 вариантов. Полный разбор всего 19 варианта (всех заданий).
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 1-5
Печи
Хозяин дачного участка строит баню с парным отделением. Парное отделение имеет размеры: длина 2,6 м, ширина 2,5 м, высота 2,2 м. Окон в парном отделении нет, для доступа внутрь планируется дверь шириной 60 см, высота дверного проёма 1,8 м. Для прогрева парного отделения можно использовать электрическую или дровяную печь. В таблице представлены характеристики трёх печей.
| Номер печи | Тип | Объём помещения (куб. м) | Масса (кг) | Стоимость (руб.) |
| 1 | дровяная | 8-13 | 42 | 19 000 |
| 2 | дровяная | 10-15,5 | 48 | 20 700 |
| 3 | электрическая | 9-15 | 15 | 16 500 |
Для установки дровяной печи дополнительных затрат не потребуется. Установка электрической печи потребует подведения специального кабеля, что обойдётся в 6200 руб.
1. Установите соответствие между объёмами помещения и номерами печей, для которых данный объём является наибольшим для отопления помещений. Заполните таблицу, в бланк ответов перенесите последовательность трёх цифр без пробелов, запятых и других дополнительных символов.
| Объём (куб. м) | 13 | 15 | 15,5 |
| Номер печи |
2. Найдите площадь пола парного отделения строящейся бани. Ответ дайте в квадратных метрах?
3. Во сколько рублей обойдётся покупка дровяной печи, подходящей по объёму ----- парного отделения, с доставкой, если доставка печи до дачного участка будет стоить 1400 рублей?
4. На электрическую печь сделали скидку 15 %. Сколько рублей стала стоить печь?
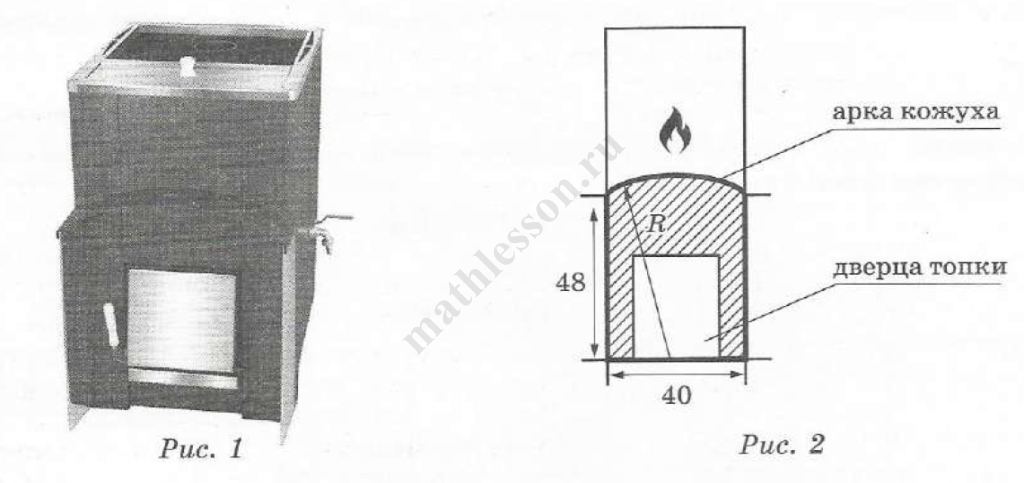
5. Хозяин выбрал дровяную печь (рис. 1). Чертёж передней панели печи показан на рисунке 2.
Печь снабжена кожухом вокруг дверцы топки. Верхняя часть кожуха выполнена в виде арки, приваренной к передней стенке печки по дуге окружности с центром в середине нижней части кожуха (рис. 2).
Для установки печки хозяину понадобилось узнать радиус закругления арки R. Размеры кожуха в сантиметрах показаны на рисунке. Найдите радиус закругления арки в сантиметрах.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 6
Найдите значение выражения $$3\cdot (\frac{5}{6}+\frac{7}{15})$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 7
Какое из данных чисел принадлежит промежутку $$[5; 6]$$?
1) $$\sqrt{5}$$
2) $$\sqrt{6}$$
3) $$\sqrt{24}$$
4) $$\sqrt{32}$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 8
Найдите значение выражения $$\sqrt{a^2 + 12ab + 36b^2}$$ при $$a = 8\frac{1}{5}$$ и $$b = \frac{4}{5}$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


$$\frac{6}{x+5}=-5$$
$$-5(x+5)=6$$
$$-5x-25=6$$
$$5x=-31$$
$$x=-\frac{31}{5}=-6,2$$
Задание 10
В фирме такси в данный момент свободно $$40$$ машин: $$17$$ чёрных, $$15$$ жёлтых и $$8$$ зелёных. Найдите вероятность того, что к заказчику приедет жёлтое такси.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 12
Площадь треугольника вычисляется по формуле $$S = \frac{1}{2}bc \cdot \sin \alpha$$, где $$b$$ и $$c$$ — две стороны треугольника, а $$\alpha$$ — угол между ними. Пользуясь этой формулой, найдите площадь $$S$$, если $$b = 16$$, $$c = 9$$ и $$\sin \alpha = \frac{1}{3}$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 14
Курс воздушных ванн начинают с $$10$$ минут в первый день и увеличивают время этой процедуры в каждый следующий день на $$5$$ минут. В какой по счёту день продолжительность процедуры достигнет $$1$$ часа $$5$$ минут?
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 15
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 16
Центр окружности, описанной около треугольника $$ABC$$, лежит на стороне $$AB$$. Радиус окружности равен $$20,5$$. Найдите $$BC$$, если $$AC = 9$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 17
Периметр ромба равен $$12$$, а один из углов равен $$30^\circ$$. Найдите площадь ромба.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 19
Какое из следующих утверждений верно?
- Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
- Сумма углов прямоугольного треугольника равна $$90^{\circ}$$ градусам.
- Любая биссектриса равнобедренного треугольника является его медианой.
В ответ запишите номер выбранного утверждения.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 20
Решите неравенство: $$(x - 7)^{2} < \sqrt{11}(x - 7)$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


$$(x-7)^{2}-\sqrt{11}(x-7)<0$$
$$(x-7)(x-7-\sqrt{11})<0$$
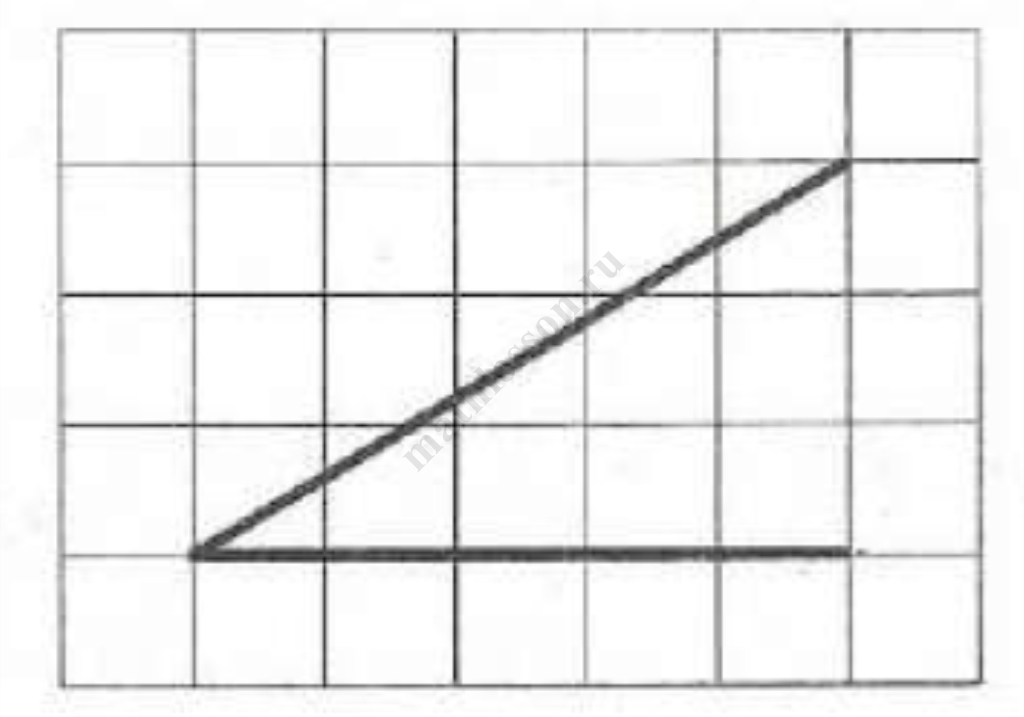
Начертим координатную прямую, отметим значения х при которых выражение $$(x-7)(x-7-\sqrt{11})$$ равно нулю и расставим знаки значений, которые принимает данное выражение на полученных промежутках:

Выберем те, в которых выражение принимает отрицательные значения: $$(7; 7+\sqrt{11})$$
Задание 21
Первая труба пропускает на $$16$$ литров воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает первая труба, если резервуар объёмом $$105$$ литров она заполняет на $$4$$ минут дольше, чем вторая труба?
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 22
Постройте график функции $$y = \left\{ \begin{aligned} -x^2 - 2x + 1,&\ x \ge -3 \\ -x - 5,&\ x < -3 \end{aligned} \right.$$ и определите, при каких значениях $$m$$ прямая $$y = m$$ имеет с графиком ровно две общие точки.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 23
В равнобедренной трапеции $$ABCD$$ с большим основанием $$AD$$ биссектриса угла $$A$$ пересекается с биссектрисой угла $$C$$ в точке $$F$$, а также пересекает сторону $$CD$$ в точке $$K$$. Известно, что угол $$AFC$$ равен $$150^{\circ}$$. Найдите $$FK$$, если $$CF=6\sqrt{3}$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 24
Известно, что около четырёхугольника $$ABCD$$ можно описать окружность и что продолжения сторон $$AD$$ и $$BC$$ четырёхугольника пересекаются в точке $$K$$. Докажите, что треугольники $$KAB$$ и $$KCD$$ подобны.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 25
На стороне $$BC$$ остроугольного треугольника $$ABC$$ ($$AB\neq AC$$) как на диаметре построена полуокружность, пересекающая высоту $$AD$$ в точке $$M$$, $$AD=80$$, $$MD=64$$, $$H$$ - точка пересечения высот треугольника $$ABC$$. Найдите $$AH$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!