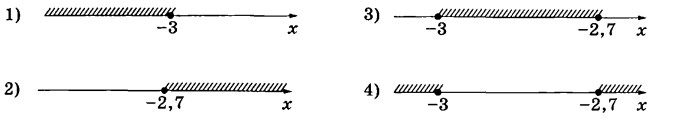ОГЭ 2023. Вариант 8 Ященко 36 вариантов ФИПИ школе.
Решаем 8 вариант ОГЭ Ященко 2023 года сборника ФИПИ школе 36 вариантов. Полный разбор всего 8 варианта (всех заданий).
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 1-5
Шины
Автомобильное колесо, как правило, представляет из себя металлический диск с установленной на него резиновой шиной. Диаметр диска совпадает с диаметром внутреннего отверстия в шине.
Для маркировки автомобильных шин применяется единая система обозначений. Например, 195/65 R15 (рис. 1). Первое число (число 195 в приведённом примере) обозначает ширину шины в миллиметрах (параметр В на рисунке 2). Второе число (число 65 в приведённом примере) — процентное отношение высоты боковины н (параметр Н на рисунке 2) к ширине шины, то есть $$100\cdot\frac{H}{B}$$.
Последующая буква обозначает тип конструкции шины. В данном примере буква R означает, что шина радиальная, то есть нити каркаса в боковине шины расположены вдоль радиусов колеса. На всех легковых автомобилях применяются шины радиальной конструкции.
За обозначением типа конструкции шины идёт число, указывающее диаметр диска колеса d в дюймах (в одном дюйме 25,4 мм). Таким образом, общий диаметр колеса D легко найти, зная диаметр диска и высоту боковины.
Возможны дополнительные маркировки, обозначающие допустимую нагрузку на шину, сезонность использования, тип дорожного покрытия и другие параметры.
Завод производит внедорожники определённой модели и устанавливает на них колёса с шинами маркировки 265/65 R18.
1. Завод допускает установку шин с другими маркировками. В таблице показаны разрешённые размеры шин.
| ширина шины (мм) | диаметр диска (дюймы) | ||
| 16 | 18 | 18 | |
| 215 | 215/65 | 215/60 | - |
| 225 | 225/65; 225/60 | 225/55 | - |
| 235 | 235/60 | 235/55; 235/50 | 235/50 |
Шины какой наибольшей ширины можно устанавливать на автомобиль, если диаметр диска равен 17 дюймам? Ответ дайте в миллиметрах.
2. На сколько миллиметров радиус колеса с шиной маркировки 215/55 R17 меньше, чем радиус колеса с шиной маркировки $$275/50$$ $$R17$$?
3. Найдите диаметр колеса автомобиля, выходящего с завода. Ответ дайте в миллиметрах.
4. На сколько миллиметров увеличится диаметр колеса, если заменить колёса, установленные на заводе, колёсами с шинами маркировки $$235/50$$ $$R18$$?
5. Сергей планирует заменить зимнюю резину на летнюю на своём автомобиле. Для каждого из четырёх колёс последовательно выполняются четыре операции: снятие колеса, замена шины, балансировка колеса и установка колеса. Он выбирает между автосервисами А и Б. Затраты на дорогу и стоимость операций даны в таблице.
| автосервис | суммарные затраты на дорогу | стоимость одного колеса | |||
| снятие колеса | замена шины | балансировка колеса | установка колеса | ||
| А | 280 руб. | 63 руб. | 255 руб. | 190 руб. | 63 руб. |
| Б | 460 руб. | 58 руб. | 225 руб. | 170 руб. | 58 руб. |
Сколько рублей заплатит Сергей за замену резины на своём автомобиле, если выберет самый дешёвый вариант?
Задание 10
В сборнике билетов по химии всего $$60$$ билетов, в $$15$$ из них встречается вопрос по теме «Кислоты». Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопрос по теме «Кислоты».
Задание 11
На рисунках изображены графики функций вида $$y = kx + b$$. Установите соответствие между графиками функций и знаками коэффициентов $$k$$ и $$b$$.
ГРАФИКИ
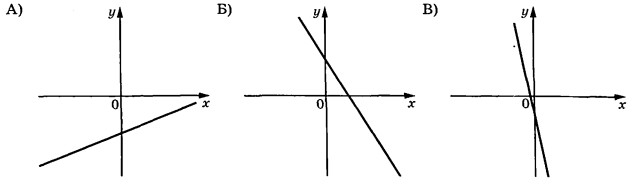
Коэффициенты:
1. $$k < 0$$, $$b > 0$$
2. $$k < 0$$, $$b < 0$$
3. $$k > 0$$, $$b < 0$$
В таблице под каждой буквой укажите соответствующий номер.
| А | Б | В |
Задание 12
В фирме «Свежесть» стоимость (в рублях) колодца из железобетонных колец рассчитывается по формуле $$C = 9500 + 7200 \cdot n$$, где $$n$$ — число колец, установленных в колодце. Пользуясь этой формулой, рассчитайте стоимость колодца из $$8$$ колец. Ответ дайте в рублях.
Задание 14
На клетчатой бумаге с размером клетки $$1 \times 1$$ нарисована «змейка», представляющая собой ломаную, состоящую из чётного числа звеньев, идущих по линиям сетки. На рисунке изображён случай, когда последнее звено имеет длину $$10$$. Найдите длину ломаной, построенной аналогичным образом, последнее звено которой имеет длину $$170$$.
Задание 15
На стороне $$AC$$ треугольника $$ABC$$ отмечена точка $$D$$ так, что $$AD = 2$$, $$DC = 7$$. Площадь треугольника $$ABC$$ равна $$27$$. Найдите площадь треугольника $$BCD$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 17
Сторона ромба равна $$12$$, а расстояние от точки пересечения диагоналей ромба до неё равно $$2$$. Найдите площадь этого ромба.
Задание 19
Какое из следующих утверждений верно?
- Средняя линия трапеции равна сумме её оснований.
- Расстояние от точки, лежащей на окружности, до центра окружности равно радиусу.
- Площадь параллелограмма равна половине произведения его диагоналей.
В ответ запишите номер выбранного утверждения.
ОДЗ: $$x^{2}+2x-15\neq0$$
$$\left\{\begin{matrix}x_{1}+x_{2}\neq-2\\x_{1}\cdot x_{2}\neq-15\end{matrix}\right.$$ $$\Leftrightarrow$$ $$\left\{\begin{matrix}x_{1}\neq-5\\x_{2}\neq3\end{matrix}\right.$$
$$\frac{-14}{(x-3)(x+5)}\leq0$$ $$\Leftrightarrow$$ $$(x-3)(x+5)>0$$
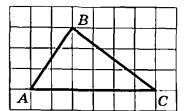
Начертим координатную прямую и отметим значения х , при которых знаменатель равен нулю (точки пустые согласно ОДЗ), расставим знаки, которые принимает выражение $$(x-3)(x+5)$$ на полученных промежутках:

Выберем промежутки, на которых выражение $$(x-3)(x+5)$$ принимает положительные значения: $$(-\infty; -5)$$ $$\cup$$ $$(3; +\infty)$$
Задание 22
Постройте график функции $$y = -1 - \frac{x - 4}{x^2 - 4x}$$. Определите, при каких значениях $$m$$ прямая $$y = m$$ не имеет с графиком общих точек.
Задание 23
Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно $$10$$, а одна из диагоналей ромба равна $$40$$. Найдите углы ромба.
Задание 24
Внутри параллелограмма $$ABCD$$ выбрали произвольную точку $$K$$. Докажите, что сумма площадей треугольников $$ABK$$ и $$CDK$$ равна половине площади параллелограмма.
Задание 25
В трапеции $$ABCD$$ боковая сторона $$AB$$ перпендикулярна основанию $$BC$$. Окружность проходит через точки $$C$$ и $$D$$ и касается прямой $$AB$$ в точке $$E$$. Найдите расстояние от точки $$E$$ до прямой $$CD$$, если $$AD=12$$, $$BC=10$$.