Задание 3816
Задание 3816
Постройте график функции $$y = -1 - \frac{x - 2}{x^2 - 4}$$ и определите, при каких значениях $$a$$ прямая $$y = a$$ не имеет с графиком ни одной общей точки.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
ОДЗ: $$x^{2}-4 \neq 0 \Leftrightarrow$$$$x\neq\pm 2$$. Преобразуем правую часть функции: $$-1-\frac{x-2}{x^{2}-4}=$$$$-1-\frac{x-2}{(x-2)(x+2)}=$$$$-1-\frac{1}{x+2}$$
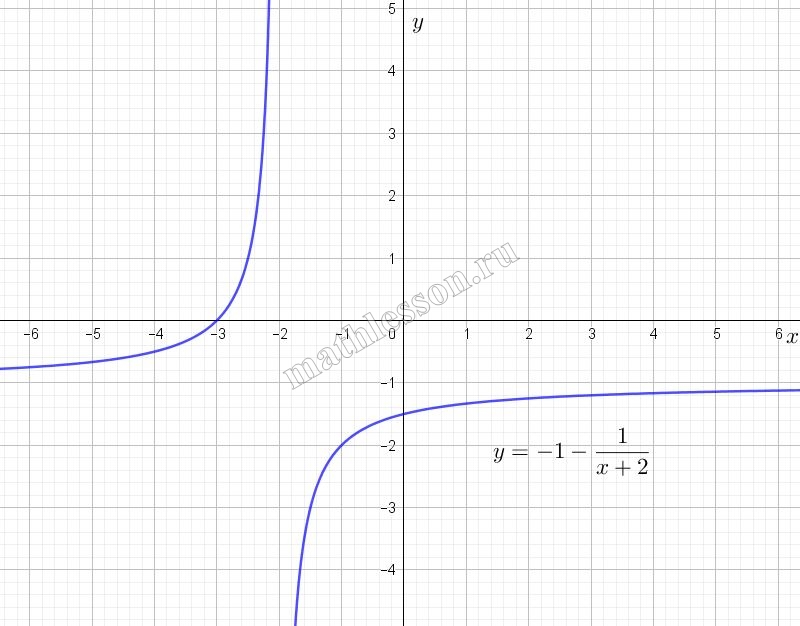
То есть график функции $$y_{1}=-1-\frac{1}{x+2}$$ и график искомой функции совпадают, если к $$y_{1}$$ применить ОДЗ для искомой. График функции $$y_{1}$$ - гипербола, смещенная на 1 единицу вних и на две влево относительно графика эталонной обратной пропорциональности $$y=\frac{1}{x}$$. Начертим график функции $$y_{1}$$:
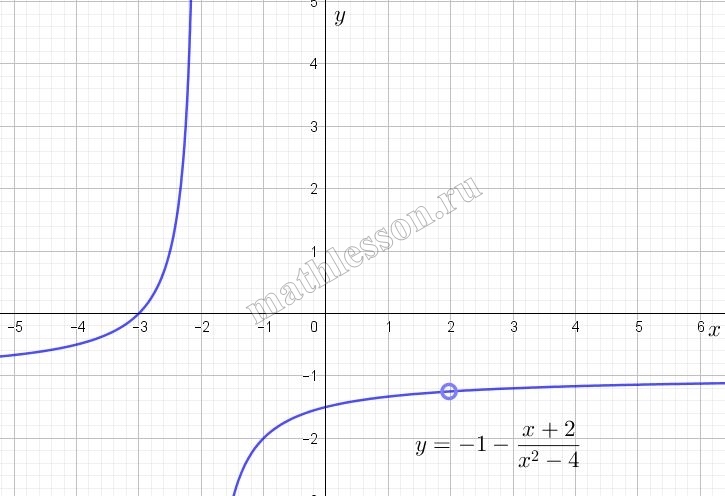
Учтем, что $$x\neq\pm 2$$. В случае $$x\neq -2$$ можно отдельно не рассматривать, так как это условие уже выполняется для графика функции $$y_{1}$$. Для $$x\neq 2$$: подставим значение $$x=2$$ в функции $$y_{1}$$: $$y_{1}(2)=-1-\frac{1}{2+2}=-\frac{5}{4}$$. То есть точку, с координатами $$(2;-\frac{5}{4})$$ необходимо отметить пустой на графике функции $$y_{1}$$ и тогда мы получим график искомой функции:
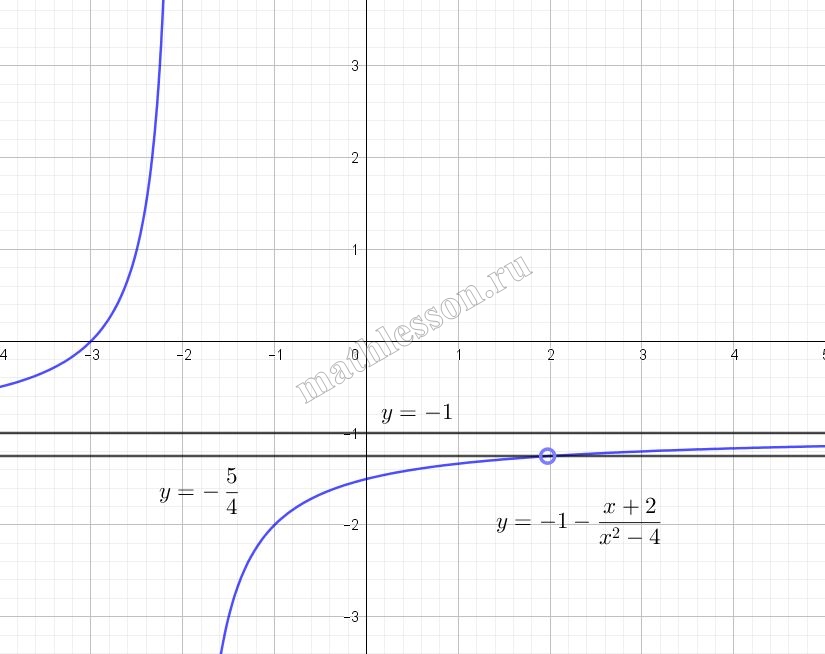
Прямая $$y=a$$ - прямая паралленая оси Ох, чтобы она не имела с графиком искомой функции точек пересечения она должны использоваться следующие значения $$a=-1;-\frac{5}{4}$$:
Аналоги к этому заданию:
Задание 4093
Постройте график функции $$y = 2 + \frac{x + 2}{x^2 + 2x}$$ и определите, при каких значениях $$m$$ прямая $$y = m$$ не имеет с графиком ни одной общей точки.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
$$y=2+\frac{x+2}{x^{2}+2x}=2+\frac{x+2}{x(x+2)}=2+\frac{1}{x}$$; $$x^{2}\neq2x\neq0$$; $$x\neq0$$; $$x\neq-2$$.
$$m=1,5$$; $$m=2$$
Задание 4173
Постройте график функции $$y = 1 - \frac{2x + 4}{x^2 + 2x}$$ и определите, при каких значениях $$a$$ прямая $$y = a$$ не имеет с графиком ни одной общей точки.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
$$y=1-\frac{2x+4}{x^{2}+2x}=1-\frac{2(x+2)}{x(x+2)}=1-\frac{2}{x}$$
$$x\neq0$$; $$x\neq2$$ $$\Rightarrow$$ $$(-2;2)$$ не входит
Тогда $$y=2$$; $$y=1$$ не имеют общих точек с $$y=1-\frac{2x+4}{x^{2}+2x}$$
Задание 3002
Постройте график функции $$y = -1 - \frac{x - 1}{x^2 - x}$$ и определите, при каких значениях $$a$$ прямая $$y = a$$ не имеет с графиком ни одной общей точки.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Упростим формулу: $$y_{1}=-1-\frac{x-1}{x(x-1)}=-1-\frac{1}{x}$$ . Следовательно , график функции $$y_{1}$$ совпадает с $$y$$ при учете , что $$x\neq 1$$.
Не имеет при $$a=-2$$ и при $$a=-1$$.
Задание 3093
Постройте график функции $$y = 1 + \frac{x - 3}{x^2 - 3x}$$ и определите, при каких значениях $$a$$ прямая $$y = a$$ не имеет с графиком ни одной общей точки.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
$$y=1+\frac{x-3}{x^{2}-3x}$$$$\Leftrightarrow$$ $$y=1+\frac{x-3}{x(x-3)}$$$$\Leftrightarrow$$ $$\left\{\begin{matrix}y=1+\frac{1}{x}\\x-3\neq 0\end{matrix}\right.$$
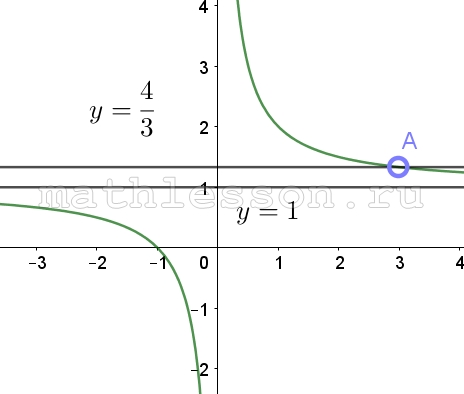
Начертим график данной функции:
Найдем оординату точки А: $$y(3)=1+\frac{1}{3}=\frac{4}{3}$$
Т.к. $$y=a$$ – прямая, параллельная Ox, то не будет иметь общих точек при $$a=\frac{4}{3}$$ (проходит через А) и $$a=1$$ (проходит через горизонтальную асимптоту)
Задание 1441
Постройте график функции $$y = 3 - \frac{x + 2}{x^2 + 2x}$$ и определите, при каких значениях $$m$$ прямая $$y = m$$ не имеет с графиком общих точек.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
