ОГЭ 2023. Вариант 19 Ященко 36 вариантов ФИПИ школе.
Решаем 19 вариант ОГЭ Ященко 2023 года сборника ФИПИ школе 36 вариантов. Полный разбор всего 19 варианта (всех заданий) Ященко 2023 ФИПИ 36 вариантов.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 1-5
Зонты
Две подруги Ира и Юля задумались о том, как рассчитать площадь поверхности зонта.
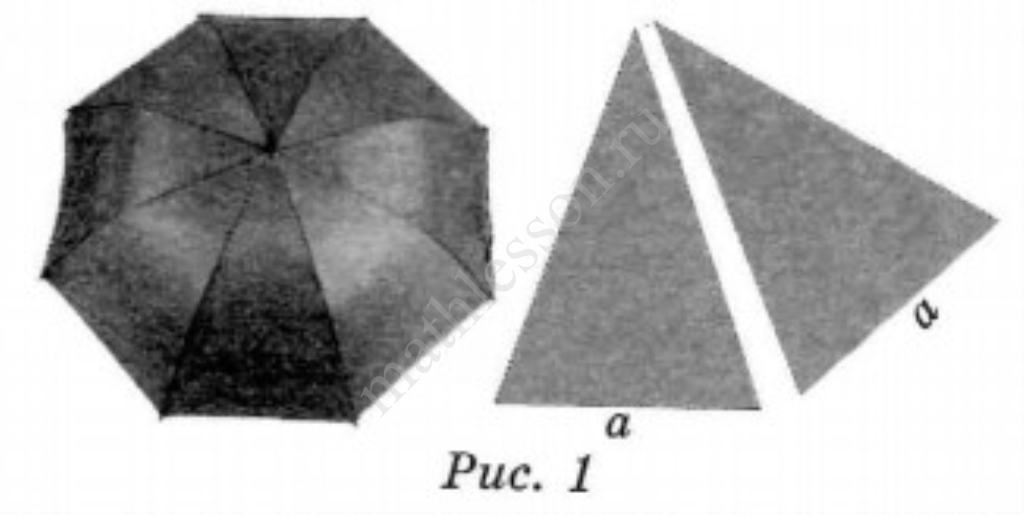
На первый взгляд зонт кажется круглым, а его купол напоминает часть сферы (сферический сегмент). Но если присмотреться, то видно, что купол зонта состоит из восьми отдельных клиньев, натянутых на каркас из восьми спиц (рис. 1). Сферическая форма в раскрытом состоянии достигается за счёт гибкости спиц и эластичности ткани, из которой изготовлен зонт.
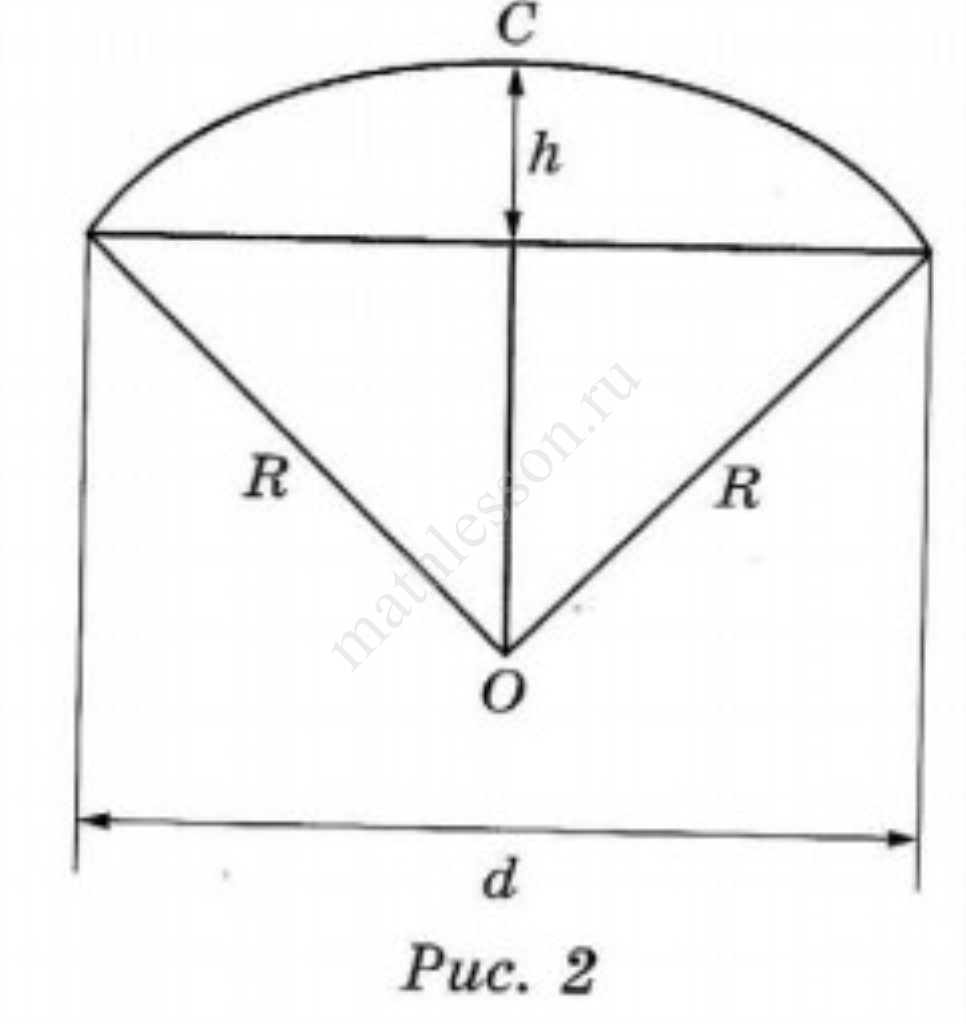
Ира и Юля сумели измерить расстояние между концами соседних спиц $$a$$. Оно оказалось равно $$40$$ см. Высота купола зонта $$h$$ (рис. 2) оказалась равна $$26$$ см, а расстояние $$d$$ между концами спиц, образующих дугу окружности, проходящей через вершину зонта, — ровно $$104$$ см.
1) Длина зонта в сложенном виде равна $$26$$ см и складывается из длины ручки (рис. 3) и трети длины спицы (зонт в три сложения). Найдите длину спицы, если длина ручки зонта равна $$6,5$$ см.
2) Поскольку зонт сшит из треугольников, рассуждала Ира, площадь его поверхности можно найти как сумму площадей треугольников. Вычислите площадь поверхности зонта методом Иры, если высота каждого равнобедренного треугольника, проведённая к основанию, равна $$55$$ см. Ответ дайте в квадратных сантиметрах.
3) Юля предположила, что купол зонта имеет форму сферического сегмента. Вычислите радиус $$R$$ сферы купола, зная, что $$OC = R$$ (рис. 2). Ответ дайте в сантиметрах.
4) Юля нашла площадь купола зонта как площадь поверхности сферического сегмента по формуле $$S=2\pi Rh$$, где $$R$$ — радиус сферы, а $$h$$ — высота сегмента. Рассчитайте площадь поверхности купола способом Юли. Число л округлите до $$3,14$$. Ответ дайте в квадратных сантиметрах с округлением до целого.
5) Рулон ткани имеет длину $$30$$ м и ширину $$90$$ см. На фабрике из этого рулона были вырезаны треугольные клинья для $$27$$ зонтов, таких же, как зонт, который был у Иры и Юли. Каждый треугольник с учётом припуска на швы имеет площадь $$1150$$ кв. см. Оставшаяся ткань пошла в обрезки. Сколько процентов ткани рулона пошло в обрезки?
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 6
Найдите значение выражения: $$\frac{1}{5}-\frac{7}{25}:\frac{2}{7}$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 7
Какое из следующих чисел заключено между числами $$-\frac{5}{17}$$ и $$-\frac{7}{19}$$?
1) $$-0,2$$
2) $$-0,3$$
3) $$-0,4$$
4) $$-0,5$$
В ответ запишите номер выбранного варианта.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 8
Найдите значение выражения $$\frac{5^9 \cdot 9^6}{45^6}$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


$$ \frac{5^9 \cdot 9^6}{45^6}=\frac{5^9 \cdot 9^6}{(5 \cdot 9)^6}=$$$$\frac{5^9 \cdot 9^6}{5^{6 \cdot 9^6}}=5^{9-6}=5^3=125$$
Задание 9
Найдите корень уравнения: $$2x^2 = 9x$$. Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 10
В девятом физико-математическом классе учатся $$13$$ мальчиков и $$7$$ девочек. По жребию они выбирают одного дежурного по классу. Какова вероятность того, что это будет мальчик?
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 12
Скорость камня (в м/с), падающего с высоты $$h$$ (в м), в момент удара о землю можно найти по формуле $$v = \sqrt{2gh}$$. Найдите скорость (в м/с), с которой ударится о землю камень, падающий с высоты $$40$$ м. Считайте, что ускорение свободного падения $$g$$ равно $$9,8$$ м/с².
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 13
Укажите решение системы неравенств:
$$\left\{\begin{aligned} -9 + 3x 0 \\ 2 - 3x -10 \end{aligned}\right.$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


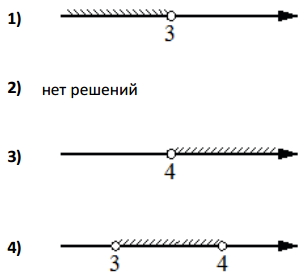
$$\left\{\begin{matrix}-9+3x< 0\\2-3x< -10\end{matrix}\right.$$ $$\Leftrightarrow$$ $$\left\{\begin{matrix}3x< 9\\-3x< -12\end{matrix}\right.$$ $$\Leftrightarrow$$ $$\left\{\begin{matrix}x< 3\\x> 4\end{matrix}\right.$$
Задание 14
Камень бросают в глубокое ущелье. При этом в первую секунду он пролетает $$13$$ метров, а в каждую следующую секунду — на $$10$$ метров больше, чем в предыдущую, до тех пор, пока не достигнет дна ущелья. Сколько метров пролетит камень за первые пять секунд?
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 16
Хорды $$AC$$ и $$BD$$ окружности пересекаются в точке $$P$$, $$BP = 9$$, $$CP = 15$$, $$DP = 20$$. Найдите $$AP$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 17
Диагонали $$AC$$ и $$BD$$ трапеции $$ABCD$$ с основаниями $$BC$$ и $$AD$$ пересекаются в точке $$O$$, $$BC = 6$$, $$AB = 13$$, $$AC = 38$$. Найдите $$AO$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 18
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 19
Какое из следующих утверждений верно?
- Боковые стороны любой трапеции равны.
- Площадь прямоугольника равна произведению длин его смежных сторон.
- Центр описанной около треугольника окружности всегда лежит внутри этого треугольника.
В ответ запишите номер выбранного утверждения.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 20
Решите неравенство: $$\frac{1}{(x - 3)^2} - \frac{3}{x - 3} - 4 = 0$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


1) Сделаем замену: $$t = \frac{1}{x - 3}.$$ Получим квадратное уравнение: $$t^2 - 3t - 4 = 0.$$
2) Дискриминант: $$D = (-3)^2 - 4\cdot 1\cdot(-4) = 9 + 16 = 25,$$ $$t_{1,2} = \dfrac{3 \pm 5}{2}.$$ То есть: $$t_1 = 4,\qquad t_2 = -1.$$
3) Возвращаемся к $$x$$:
1) $$\frac{1}{x - 3} = 4,$$ $$x - 3 = \frac{1}{4},$$ $$x = \frac{13}{4} = 3{,}25.$$
2) $$\frac{1}{x - 3} = -1,$$ $$x - 3 = -1,$$ $$x = 2.$$
Задание 21
Велосипедист выехал с постоянной скоростью из города $$A$$ в город $$B$$, расстояние между которыми равно $$209$$ км. На следующий день он отправился обратно в $$A$$, увеличив скорость на $$8$$ км/ч. По пути он сделал остановку на $$8$$ часа, в результате чего затратил на обратный путь столько же времени, сколько на путь из $$A$$ в $$B$$. Найдите скорость велосипедиста на пути из $$B$$ в $$A$$.
Задание 22
Постройте график функции $$y = \frac{(x^2 + x - 6)(x^2 - 2x - 3)}{x^2 - 9}$$ и определите, при каких значениях $$m$$ прямая $$y = m$$ имеет с графиком ровно одну общую точку.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 23
Биссектрисы углов $$A$$ и $$B$$ при боковой стороне $$AB$$ трапеции $$ABCD$$ пересекаются в точке $$F$$. Найдите $$AB$$, если $$AF=21$$, $$BF=20$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 25
Точки $$M$$ и $$N$$ лежат на стороне $$AC$$ треугольника $$ABC$$ на расстояниях соответственно $$9$$ и $$11$$ от вершины $$A$$. Найдите радиус окружности, проходящей через точки $$M$$ и $$A$$ и касающейся луча $$AB$$, если $$\cos \angle BAC=\frac{\sqrt{11}}{6}$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!