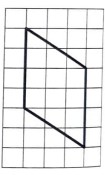
ОГЭ 2024. Вариант 2 Ященко 36 вариантов ФИПИ школе.
Решаем 2 вариант ОГЭ Ященко 2024 года сборника ФИПИ школе 36 вариантов. Полный разбор всего 2 варианта (всех заданий) Ященко 2024 ФИПИ 36 вариантов.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 1-5
Листы
Общепринятые форматы листов бумаги обозначают буквой А и цифрой: АО, А1, А2 и так далее. Если лист формата АО разрезать пополам, получаются два листа формата А1. Если лист А1 разрезать пополам, получаются два листа формата А2 и так далее. При этом отношение длины листа к его ширине у всех форматов, обозначенных буквой А, одно и то же (то есть листы всех форматов подобны друг другу). Это сделано специально — чтобы можно было сохранить пропорции текста на листе при изменении формата бумаги (размер шрифта при этом тоже соответственно изменяется).
В таблице 1 даны размеры листов бумаги четырёх форматов: от АЗ до А6.
Таблица 1
| Порядковые номера | Ширина (мм) | Длина (мм) |
| 1 | 148 | 210 |
| 2 | 297 | 420 |
| 3 | 105 | 148 |
| 4 | 210 | 297 |
Задание 1.
Для листов бумаги форматов А6, А5, А4 и АЗ определите, какими порядковыми номерами обозначены их размеры в таблице 1. Заполните таблицу ниже, в бланк ответов перенесите последовательность четырёх цифр.
| Форматы бумаги | А6 | А5 | А4 | АЗ |
| Порядковые номера |
Задание 2.
Сколько листов бумаги формата А5 получится при разрезании одного листа бумаги формата А2?
Задание 3.
Найдите длину меньшей стороны листа бумаги формата А1. Ответ дайте в миллиметрах.
Задание 4.
Найдите площадь листа бумаги формата А6. Ответ дайте в квадратных сантиметрах.
Задание 5.
Найдите отношение длины меньшей стороны листа к большей у бумаги формата А2. Ответ дайте с точностью до десятых.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 8
Найдите значение выражения $$\sqrt{(-b)^8 \cdot b^2}$$ при $$b = 2$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 9
Решите уравнение: $$5x^2 - 2x - 3 = 0$$. Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 10
В фирме такси в данный момент свободно $$40$$ машин: $$7$$ чёрных, $$19$$ жёлтых и $$14$$ зелёных. Найдите вероятность того, что к заказчику приедет зелёное такси.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 11
На рисунках изображены графики функций вида $$y = ax^2 + bx + c$$. Установите соответствие между графиками функций и знаками коэффициентов $$a$$ и $$c$$.
Коэффициенты:
1. $$a < 0$$, $$c > 0$$
2. $$a > 0$$, $$c < 0$$
3. $$a > 0$$, $$c > 0$$
ГРАФИКИ
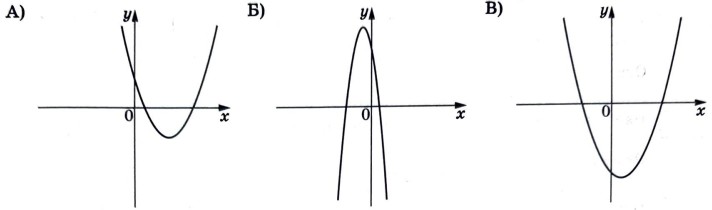
В таблице под каждой буквой укажите соответствующий номер.
| А | Б | В |
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 12
Мощность постоянного тока (в ваттах) вычисляется по формуле $$P = I^2 R$$, где $$I$$ — сила тока (в амперах), $$R$$ — сопротивление (в омах). Пользуясь этой формулой, найдите сопротивление $$R$$, если мощность составляет $$144,5$$ Вт, а сила тока равна $$8,5$$ А. Ответ дайте в омах.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 13
Укажите решение неравенства: $$5x - 3(5x - 8) -7$$
1) $$( -\infty;\ 3,1 )$$
2) $$( -1,7;\ +\infty )$$
3) $$( -\infty;\ -1,7 )$$
4) $$( 3,1;\ +\infty )$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 14
В ходе бета-распада радиоактивного изотопа A каждые $$8$$ минут половина его атомов без потери массы преобразуются в атомы стабильного изотопа B. В начальный момент масса изотопа A составляла $$320$$ мг. Найдите массу образовавшегося изотопа B через $$40$$ минут. Ответ дайте в миллиграммах.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 15
Медиана равностороннего треугольника равна $$12\sqrt{3}$$. Найдите сторону этого треугольника.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 16
Трапеция $$ABCD$$ с основаниями $$AD$$ и $$BC$$ описана около окружности, $$AB = 15$$, $$BC = 20$$, $$CD = 17$$. Найдите $$AD$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 17
Сумма двух углов равнобедренной трапеции равна $$218^\circ$$. Найдите меньший угол этой трапеции. Ответ дайте в градусах.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 19
Какое из следующих утверждений верно?
- В параллелограмме есть два равных угла.
- Каждая из биссектрис равнобедренного треугольника является его медианой.
- Площадь прямоугольного треугольника равна произведению длин его катетов.
В ответ запишите номер выбранного утверждения.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
1) Группируем: $$x^3 + 5x^2 - 4x - 20 = x^2(x+5) - 4(x+5).$$
2) Выносим общий множитель: $$(x+5)(x^2 - 4) = 0.$$
3) Раскладываем квадратный множитель: $$x^2 - 4 = (x-2)(x+2),$$ поэтому $$(x+5)(x-2)(x+2) = 0.$$
4) Приравниваем множители к нулю: $$x+5 = 0,\quad x-2 = 0,\quad x+2 = 0,$$ получаем $$x = -5,\; 2,\; -2.$$
Задание 21
Два автомобиля одновременно отправляются в $$475$$ - километровый пробег. Первый едет со скоростью на $$18$$ км/ч большей, чем второй, и прибывает к финишу на $$2$$ ч раньше второго. Найдите скорость первого автомобиля.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 22
Постройте график функции $$y = \frac{(0{,}5x^2 + 0{,}5x) \cdot |x|}{x + 1}$$. Определите, при каких значениях $$m$$ прямая $$y = m$$ не имеет с графиком ни одной общей точки.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 23
Углы $$B$$ и $$C$$ треугольника $$ABC$$ равны соответственно $$61^{\circ}$$ и $$89^{\circ}$$. Найдите $$BC$$, если радиус окружности, описанной около треугольника $$ABC$$, равен $$10$$.
По сумме углов треугольника:
$$\angle A=180^{\circ}-61^{\circ}-89^{\circ}=30^{\circ}$$
По теореме синусов:
$$2R=\frac{BC}{\sin A}$$
$$BC=2R\cdot\sin A=2\cdot 10\cdot\sin 30^{\circ}=2\cdot 10\cdot 0.5=10$$
Задание 24
В трапеции $$MNPK$$ с основаниями $$NP$$ и $$MK$$ диагонали пересекаются в точке $$F$$. Докажите, что площади треугольников $$MNF$$ и $$PKF$$ равны.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 25
В треугольнике $$ABC$$ биссектриса $$BE$$ и медиана $$AD$$ перпендикулярны и имеют одинаковую длину, равную $$20$$. Найдите стороны треугольника $$ABC$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!