ОГЭ 2022. Вариант 7 Ященко 36 вариантов ФИПИ школе.
Решаем 7 вариант ОГЭ Ященко 2022 года сборника ФИПИ школе 36 вариантов. Полный разбор всего 7 варианта (всех заданий).
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 1-5
План местности
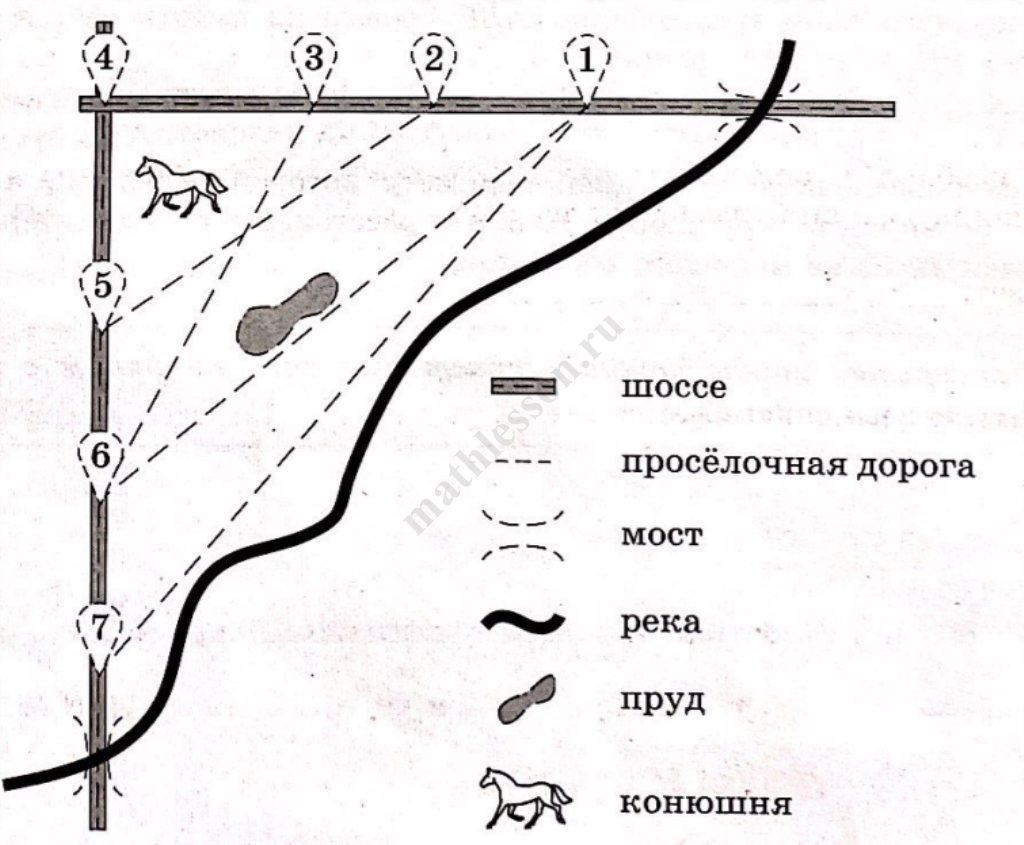
На рисунке изображён план сельской местности. Таня на летних каникулах приезжает в гости к дедушке в деревню Антоновку (на плане обозначена цифрой 1). В конце каникул дедушка на машине собирается отвезти Таню на автобусную станцию, которая находится в деревне Богданово. Из Антоновки в Богданово можно проехать по просёлочной дороге вдоль реки. Есть другой путь — по шоссе до деревни Ванютино, где нужно повернуть под прямым углом налево на другое шоссе, ведущее в Богданово. Третий маршрут проходит по просёлочной дороге мимо пруда до деревни Горюново, где можно свернуть на шоссе до Богданово. Четвёртый маршрут пролегает по шоссе до деревни Доломино, от Доломино до Горюново по просёлочной дороге мимо конюшни и от Горюново до Богданово по шоссе. Ещё один маршрут проходит по шоссе до деревни Егорки, по просёлочной дороге мимо конюшни от Егорки до Жилино и по шоссе от Жилино до Богданово.
Шоссе и просёлочные дороги образуют прямоугольные треугольники.
По шоссе Таня с дедушкой едут со скоростью 50 км/ч, а по просёлочным дорогам — со скоростью 30 км/ч. Расстояние от Антоновки до Доломино равно 12 км, от Доломино до Егорки — 4 км, от Егорки до Ванютино — 12 км, от Горюново до Ванютино — 15 км, от Ванютино до Жилино — 9 км, а от Жилино до Богданово — 12 км.
1) Пользуясь описанием, определите, какими цифрами на плане обозначены деревни. Заполните таблицу, в бланк ответов перенесите последовательность четырёх цифр без пробелов, запятых и других дополнительных символов.
| Деревни | д. Богданово | д. Горюново | д. Доломино | д. Егорка |
| Цифры |
2) Найдите расстояние от Антоновки до Богданово по прямой. Ответ дайте в километрах.
3) Сколько минут затратят на дорогу Таня с дедушкой из Антоновки в Богданово, если поедут через Егорку и Жилино мимо конюшни?
4) За какое наименьшее количество минут Таня с дедушкой могут добраться из Доломино в Горюново?
5) На просёлочных дорогах машина дедушки расходует 8,2 литра бензина на 100 км. Известно, что на путь из Антоновки до Богданово через Ванютино и путь напрямик ей необходим один и тот же объём бензина. Сколько литров бензина на 100 км машина дедушки расходует на шоссе?
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 6
Между какими целыми числами заключено число $$\frac{170}{19}$$?
1) $$8$$ и $$9$$
2) $$9$$ и $$10$$
3) $$10$$ и $$11$$
4) $$11$$ и $$12$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 7
Найдите значение выражения $$\sqrt{\frac{1}{25} \cdot x^4 \cdot y^8}$$ при $$x = 5$$, $$y = 2$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 9
В среднем из каждых $$60$$ поступивших в продажу аккумуляторов $$51$$ — заряжен. Найдите вероятность того, что выбранный в магазине наудачу аккумулятор не заряжен.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 10
На рисунках изображены графики функций вида $$y = ax^2 + bx + c$$. Установите соответствие между графиками функций и знаками коэффициентов $$a$$ и $$c$$.
Коэффициенты
1. $$a < 0$$, $$c > 0$$
2. $$a > 0$$, $$c > 0$$
3. $$a > 0$$, $$c < 0$$
ГРАФИКИ
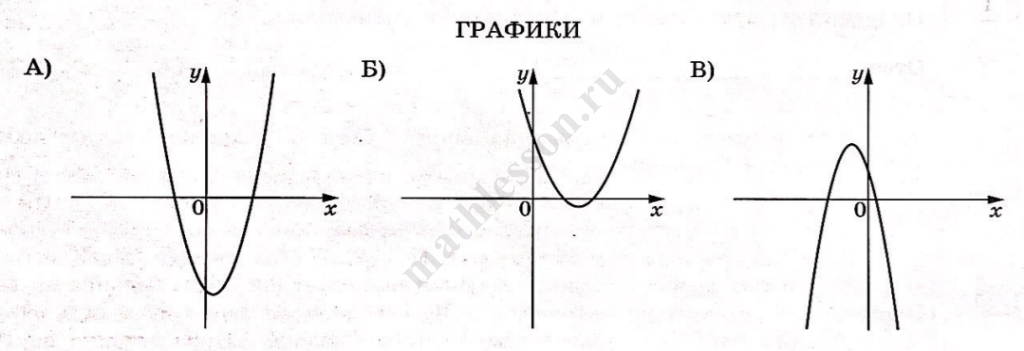
В таблице под каждой буквой укажите соответствующий номер.
| А | Б | В |
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 11
Радиус вписанной в прямоугольный треугольник окружности вычисляется по формуле $$r = \frac{a + b - c}{2}$$, где $$a$$ и $$b$$ — катеты, а $$c$$ — гипотенуза. Пользуясь этой формулой, найдите $$c$$, если $$a = 20$$, $$b = 21$$ и $$r = 6$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 12
Укажите решение неравенства: $$5x - x^2 > 0$$
1) $$( -\infty;\ 0 ) \cup ( 5;\ +\infty )$$
2) $$( 0;\ 5 )$$
3) $$( 5;\ +\infty )$$
4) $$( 0;\ +\infty )$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 13
В ходе биологического эксперимента в чашку Петри с питательной средой поместили колонию микроорганизмов массой $$3$$ мг. Каждые $$20$$ минут масса колонии увеличивается в $$3$$ раза. Найдите массу колонии микроорганизмов через $$80$$ минут после начала эксперимента. Ответ дайте в миллиграммах.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 14
В треугольнике $$ABC$$ известно, что $$AB = 5$$, $$BC = 10$$, $$AC = 11$$. Найдите $$\cos ABC$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 15
Через точку $$A$$, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке $$K$$. Другая прямая пересекает окружность в точках $$B$$ и $$C$$, причём $$AB = 4$$, $$AC = 64$$. Найдите $$AK$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 16
Основания трапеции равны $$8$$ и $$18$$, а высота равна $$5$$. Найдите среднюю линию этой трапеции.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 18
Какие из следующих утверждений верны?
- Длина гипотенузы прямоугольного треугольника меньше суммы длин его катетов.
- В тупоугольном треугольнике все углы тупые.
- Средняя линия трапеции равна полусумме её оснований.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Задание 19
Решите систему уравнений: $$\left\{\begin{aligned} (x - 8)(y - 9) = 0 \\ \frac{y - 5}{x + y - 13} = 4 \end{aligned}\right.$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


1) Пусть $$x = 8.$$ Тогда $$\dfrac{y - 5}{8 + y - 13} = 4 \;\Rightarrow\; \dfrac{y - 5}{y - 5} = 4.$$ Если $$y \neq 5,$$ получаем противоречие $$1 = 4.$$ Если $$y = 5,$$ знаменатель равен нулю, выражение не определено. Следовательно, решений при $$x = 8$$ нет.
2) Пусть $$y = 9.$$ Тогда $$\dfrac{9 - 5}{x + 9 - 13} = 4 \;\Rightarrow\; \dfrac{4}{x - 4} = 4.$$ Отсюда $$\dfrac{4}{x - 4} = 4 \;\Rightarrow\; \dfrac{1}{x - 4} = 1 \;\Rightarrow\; x - 4 = 1 \;\Rightarrow\; x = 5.$$ Проверяем знаменатель: $$x + y - 13 = 5 + 9 - 13 = 1 \neq 0.$$ Решение подходит.
Задание 20
Расстояние между пристанями $$A$$ и $$B$$ равно $$45$$ км. Из $$A$$ в $$B$$ по течению реки отправился плот, а через час вслед за ним отправилась моторная лодка, которая, прибыв в пункт $$B$$, тотчас повернула обратно и возвратилась в $$A$$. К этому времени плот проплыл $$28$$ км. Найдите скорость моторной лодки в неподвижной воде, если скорость течения реки равна $$4$$ км/ч. Ответ дайте в км/ч.
Задание 21
Постройте график функции $$y = 4|x + 2| - x^2 - 3x - 2$$. Определите, при каких значениях $$m$$ прямая $$y = m$$ имеет с графиком ровно три общие точки.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 23
Через точку $$O$$ пересечения диагоналей параллелограмма $$ABCD$$ проведена прямая, пересекающая стороны $$BC$$ и $$AD$$ в точках $$K$$ и $$M$$ соответственно. Докажите, что отрезки $$BK$$ и $$DM$$ равны.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 24
Четырёхугольник $$ABCD$$ со сторонами $$AB=40$$ и $$CD=10$$ вписан в окружность. Диагонали $$AC$$ и $$BD$$ пересекаются в точке $$K$$, причём $$\angle AKB=60^{\circ}$$. Найдите радиус окружности, описанной около этого четырёхугольника.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!