ОГЭ 2022. Вариант 8 Ященко 36 вариантов ФИПИ школе.
Решаем 8 вариант ОГЭ Ященко 2022 года сборника ФИПИ школе 36 вариантов. Полный разбор всего 8 варианта (всех заданий).
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 1-5
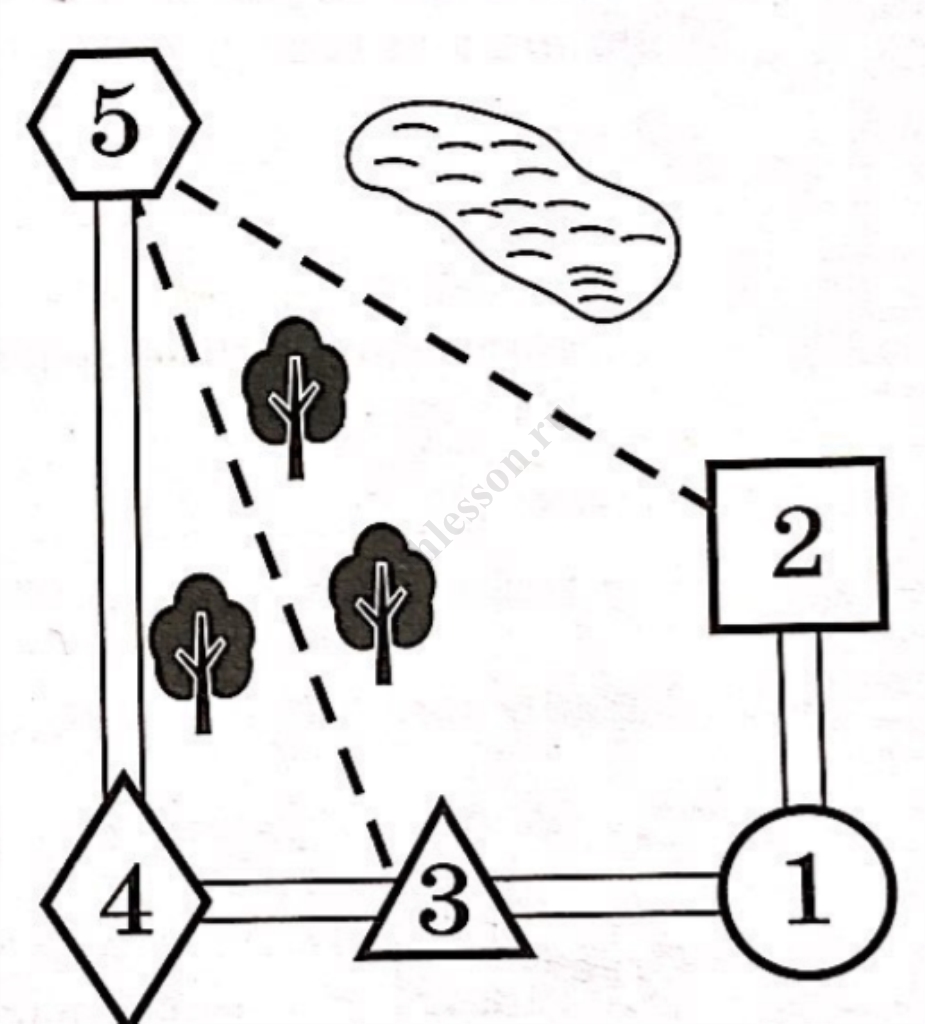
План местности
Юля летом отдыхает у дедушки и бабушки в деревне Царёво. Юля с дедушкой собираются съездить на машине на железнодорожную станцию Таировку. Из Царёво в Таировку можно проехать по шоссе до деревни Ключи, где нужно свернуть под прямым углом налево на другое шоссе, ведущее в Таировку через посёлок Демидово. Из Царёво в Таировку можно проехать через посёлок Демидово и не заезжая в Ключи, но тогда первую часть пути надо будет ехать по прямой лесной дороге. Есть и третий маршрут: доехать по прямой грунтовой дороге мимо озера до села Федяево и там, повернув направо, по шоссе добраться до Таировки.
По шоссе Юля с дедушкой едут со скоростью 60 км/ч, а по лесной и грунтовой дорогам —45 км/ч. Расстояние по шоссе от Царёво до Ключей равно 72 км, от Таировки до Ключей — 60 км, от Таировки до Демидово — 30 км, а от Таировки до Федяево — 27 км.
1) Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты. В ответ запишите полученную последовательность пяти цифр
| Насел, пункты | п. Демидово | д. Ключи | ст. Таировка | с. Федяево | д. Царёво |
| Цифры |
2) Найдите расстояние от деревни Царёво до посёлка Демидово по лесной дороге. Ответ дайте в километрах.
3) Сколько минут затратят на дорогу Юля с дедушкой, если поедут на станцию через Ключи?
4) Определите, на какой маршрут до станции потребуется меньше всего времени. В ответе укажите, сколько минут потратят на дорогу Юля с дедушкой, если поедут этим маршрутом.
5) На шоссе машина дедушки расходует 6,5 литра бензина на 100 км. Известно, что на путь из Царёво до Таировки через Ключи и на путь через Федяево ей необходим один и тот же объём бензина. Сколько литров бензина на 100 км машина дедушки расходует на грунтовых дорогах?
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 7
Между какими целыми числами заключено число $$\frac{140}{17}$$?
1) $$5$$ и $$6$$
2) $$6$$ и $$7$$
3) $$7$$ и $$8$$
4) $$8$$ и $$9$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 8
Найдите значение выражения $$\sqrt{\frac{1}{16} \cdot x^{10} \cdot y^2}$$ при $$x = 2$$, $$y = 3$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 10
В среднем из каждых $$50$$ поступивших в продажу аккумуляторов $$47$$ аккумуляторов заряжены. Найдите вероятность того, что выбранный в магазине наудачу аккумулятор не заряжен.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 11
На рисунках изображены графики функций вида $$y = ax^2 + bx + c$$. Установите соответствие между знаками коэффициентов $$a$$ и $$c$$ и графиками функций.
Коэффициенты
А. $$a > 0$$; $$c < 0$$
Б. $$a > 0$$; $$c > 0$$
В. $$a < 0$$; $$c > 0$$
ГРАФИКИ
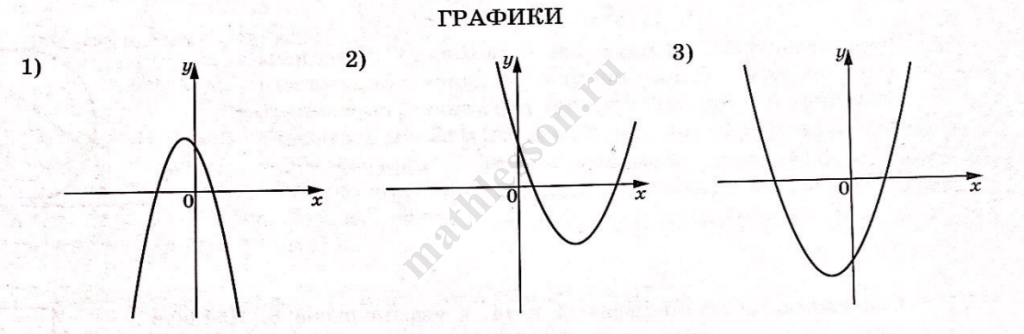
В таблице под каждой буквой укажите соответствующий номер.
| А | Б | В |
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 12
Радиус вписанной в прямоугольный треугольник окружности вычисляется по формуле $$r = \frac{a + b - c}{2}$$, где $$a$$ и $$b$$ — катеты, а $$c$$ — гипотенуза. Пользуясь этой формулой, найдите $$c$$, если $$a = 12$$, $$b = 35$$ и $$r = 5$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 13
Укажите решение неравенства: $$6x - x^2 \ge 0$$
1) $$[ 0;\ +\infty )$$
2) $$( -\infty;\ 0 ] \cup [ 6;\ +\infty )$$
3) $$[ 0;\ 6 ]$$
4) $$[ 6;\ +\infty )$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 14
В ходе биологического эксперимента в чашку Петри с питательной средой поместили колонию микроорганизмов массой $$16$$ мг. Каждые $$20$$ минут масса колонии увеличивается в $$3$$ раза. Найдите массу колонии микроорганизмов через $$60$$ минут после начала эксперимента. Ответ дайте в миллиграммах.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 16
Через точку $$A$$, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке $$K$$. Другая прямая пересекает окружность в точках $$B$$ и $$C$$, причём $$AB = 4$$, $$BC = 12$$. Найдите $$AK$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 17
Основания трапеции равны $$4$$ и $$14$$, а высота равна $$8$$. Найдите среднюю линию этой трапеции.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 19
Какие из следующих утверждений верны?
- Через заданную точку плоскости можно провести только одну прямую.
- Серединные перпендикуляры к сторонам треугольника пересекаются в точке, являющейся центром окружности, описанной около этого треугольника.
- Если в параллелограмме две соседние стороны равны, то этот параллелограмм является ромбом.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 20
Решите систему уравнений: $$ \left\{ \begin{aligned} (x - 4)(y - 7) = 0\\ \frac{y - 5}{x + y - 9} = 2 \end{aligned} \right. $$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Из первого уравнения получаем: $$(x-4)(y-7)=0 \Rightarrow x=4$$ или $$y=7.$$
1) Пусть $$x=4.$$ Подставим во второе уравнение: $$\dfrac{y-5}{4+y-9}=2 \;\Rightarrow\; \dfrac{y-5}{y-5}=2.$$ Если $$y\neq5,$$ то левая часть равна $$1,$$ получаем противоречие $$1=2.$$ Если $$y=5,$$ то знаменатель равен нулю, дробь не имеет смысла. Следовательно, при $$x=4$$ решений нет.
2) Пусть $$y=7.$$ Подставим во второе уравнение: $$\dfrac{7-5}{x+7-9}=2 \;\Rightarrow\; \dfrac{2}{x-2}=2.$$ Отсюда $$\dfrac{2}{x-2}=2 \;\Rightarrow\; \dfrac{1}{x-2}=1 \;\Rightarrow\; x-2=1 \;\Rightarrow\; x=3.$$ Проверим знаменатель: $$x+y-9=3+7-9=1\neq 0.$$ Значит, пара $$(3;7)$$ является решением системы.
Задание 21
Расстояние между пристанями $$A$$ и $$B$$ равно $$60$$ км. Из $$A$$ в $$B$$ по течению реки отправился плот, а через час вслед за ним отправилась моторная лодка, которая, прибыв в пункт $$B$$, тотчас повернула обратно и возвратилась в $$A$$. К этому времени плот проплыл $$30$$ км. Найдите скорость моторной лодки в неподвижной воде, если скорость течения реки равна $$5$$ км/ч. Ответ дайте в км/ч.
Задание 23
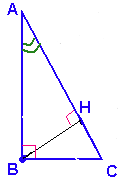
Точка $$H$$ является основанием высоты, проведённой из вершины прямого угла $$B$$ треугольника $$ABC$$ к гипотенузе $$AC$$. Найдите $$AB$$, если $$AH=9$$, $$AC=36$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 24
Биссектрисы углов $$A$$ и $$D$$ трапеции $$ABCD$$ пересекаются в точке $$M$$, лежащей на стороне $$BC$$. Докажите, что точка $$M$$ равноудалена от прямых $$AB$$, $$AD$$ и $$CD$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 25
Четырёхугольник $$ABCD$$ со сторонами $$AB=12$$ и $$CD=30$$ вписан в окружность. Диагонали $$AC$$ и $$BD$$ пересекаются в точке $$K$$, причём $$\angle AKB=60^{\circ}$$. Найдите радиус окружности, описанной около этого четырёхугольника.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!