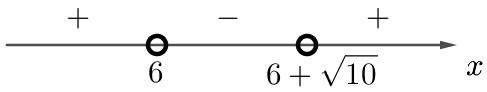ОГЭ 2024. Вариант 6 Ященко 36 вариантов ФИПИ школе.
Решаем 6 вариант ОГЭ Ященко 2024 года сборника ФИПИ школе 36 вариантов. Полный разбор всего 6 варианта (всех заданий) Ященко 2024 ФИПИ 36 вариантов.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 1-5
Печи
Хозяин дачного участка строит баню с парным отделением. Парное отделение имеет размеры: длина 2,8 м, ширина 2,5 м, высота 2 м. Окон в парном отделении нет, для доступа внутрь планируется дверь шириной 60 см, высота дверного проёма 1,8 м. Для прогрева парного отделения можно использовать электрическую или дровяную печь. В таблице представлены характеристики трёх печей.
| Номер печи | Тип | Объём помещения (куб. м) | Масса (кг) | Стоимость (руб.) |
| 1 | дровяная | 9-13 | 40 | 18500 |
| 2 | дровяная | 10-16 | 46 | 20500 |
| 3 | электрическая | 9-15 | 16 | 16000 |
Для установки дровяной печи дополнительных затрат не потребуется. Установка электрической печи потребует подведения специального кабеля, что обойдётся в 5500 руб.
1. Установите соответствие между объёмами помещения и номерами печей, для которых данный объём является наибольшим для отопления помещений.
Заполните таблицу, в бланк ответов перенесите последовательность трёх цифр без пробелов, запятых и других дополнительных символов.
| Объём помещения (куб. м) | 16 | 13 | 15 |
| Номер печи |
2. Найдите площадь пола парного отделения строящейся бани. Ответ дайте в квадратных метрах.
3. Во сколько рублей обойдётся покупка электрической печи с установкой и доставкой, если доставка печи до дачного участка будет стоить 1700 рублей?
4. В прошлом году печи, указанные в таблице, стоили дороже. На них были сделаны скидки: на печь номер 1 скидка составила 25%, на печь номер 2 - 10%, на печь номер 3 - 20%. Сколько рублей стоила печь номер 3 в прошлом году?
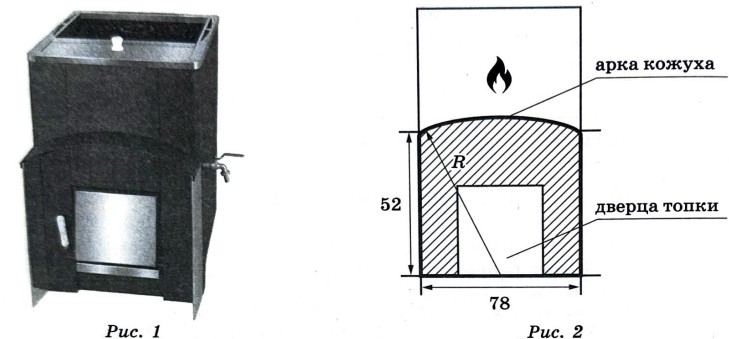
5. Хозяин выбрал дровяную печь (рис. 1). Чертёж передней панели печи показан на рисунке 2.
Печь снабжена кожухом вокруг дверцы топки. Верхняя часть кожуха выполнена в виде арки, приваренной к передней стенке печки по дуге окружности с центром в середине нижней части кожуха (см. рис. 2). Для установки печки хозяину понадобилось узнать радиус закругления арки $$R$$. Размеры кожуха в сантиметрах показаны на рисунке. Найдите радиус закругления арки в сантиметрах.
Задание 10
В соревнованиях по толканию ядра участвуют $$4$$ спортсмена из Японии, $$5$$ — из Вьетнама, $$8$$ — из Китая и $$3$$ — из Монголии. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что последним будет выступать спортсмен из Монголии.
Задание 12
Работа постоянного тока (в джоулях) вычисляется по формуле $$A = \frac{U^2 t}{R}$$, где $$U$$ — напряжение (в вольтах), $$R$$ — сопротивление (в омах), $$t$$ — время (в секундах). Пользуясь этой формулой, найдите $$A$$ (в джоулях), если $$t = 15$$ с, $$U = 6$$ В и $$R = 9$$ Ом.
Задание 19
Какое из следующих утверждений верно?
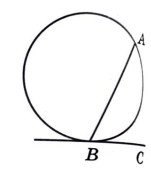
- Точка пересечения двух окружностей равноудалена от центров этих окружностей.
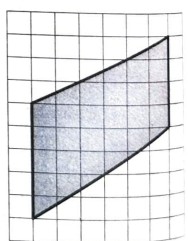
- В параллелограмме есть два равных угла.
- Площадь прямоугольного треугольника равна произведению длин его катетов.
В ответ запишите номер выбранного утверждения.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 20
Решите неравенство: $$36 - 12x + x^2 \sqrt{10}(x - 6)$$
1) Перенесём всё в левую часть: $$x^2 - 12x + 36 - \sqrt{10}(x - 6) < 0.$$
Учтем, что $$x^2 - 12x + 36 = (x - 6)^2$$. Тогда $$(x - 6)^2 - \sqrt{10}(x - 6) < 0.$$ Вынесём общий множитель: $$(x - 6)\bigl((x - 6) - \sqrt{10}\bigr) < 0,$$ $$(x - 6)(x - 6 - \sqrt{10}) < 0$$
2) Найдём нули выражения: $$x_1 = 6; x_2 = 6 + \sqrt{10}.$$ Отметим их на координатной прямой. Расставим знаки, которые принимает выражение $$(x - 6)(x - 6 - \sqrt{10})$$ на полученных интервалах:
Выражение отрицательно при: $$x \in (6;\, 6 + \sqrt{10}).$$