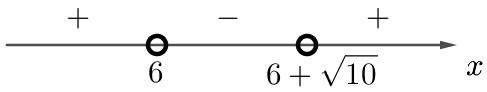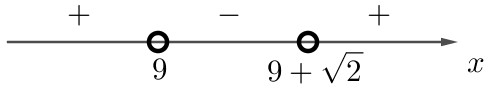Задание 295
Задание 295
Решите неравенство: $$36 - 12x + x^2 \sqrt{10}(x - 6)$$
1) Перенесём всё в левую часть: $$x^2 - 12x + 36 - \sqrt{10}(x - 6) < 0.$$
Учтем, что $$x^2 - 12x + 36 = (x - 6)^2$$. Тогда $$(x - 6)^2 - \sqrt{10}(x - 6) < 0.$$ Вынесём общий множитель: $$(x - 6)\bigl((x - 6) - \sqrt{10}\bigr) < 0,$$ $$(x - 6)(x - 6 - \sqrt{10}) < 0$$
2) Найдём нули выражения: $$x_1 = 6; x_2 = 6 + \sqrt{10}.$$ Отметим их на координатной прямой. Расставим знаки, которые принимает выражение $$(x - 6)(x - 6 - \sqrt{10})$$ на полученных интервалах:
Выражение отрицательно при: $$x \in (6;\, 6 + \sqrt{10}).$$
Аналоги к этому заданию:
Задание 315
Решите неравенство: $$81 - 18x + x^2 \sqrt{2}(x - 9)$$
1) Перенесём всё в левую часть: $$x^2 - 18x + 81 - \sqrt{2}(x - 9) < 0.$$ Замечаем, что $$(x - 9)^2 - \sqrt{2}(x - 9) < 0.$$ Вынесём общий множитель: $$(x - 9)\bigl((x - 9) - \sqrt{2}\bigr) < 0,$$ $$(x - 9)(x - 9 - \sqrt{2}) < 0,$$
2) Нули: $$x_1 = 9,\qquad x_2 = 9 + \sqrt{2}.$$ Отметим их на координатной прямой. Расставим знаки, которые принимает выражение $$(x - 9)(x - 9 - \sqrt{2})$$ на полученных интервалах:
Выражение отрицательно при: $$x \in (9;\, 9 + \sqrt{2}).$$