Задание 1550
Задание 1550
Боковые стороны $$AB$$ и $$CD$$ трапеции $$ABCD$$ равны соответственно $$24$$ и $$25$$, а основание $$BC$$ равно $$9$$. Биссектриса угла $$ADC$$ проходит через середину стороны $$AB$$. Найдите площадь трапеции.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Аналоги к этому заданию:
Задание 4172
Боковые стороны $$AB$$ и $$CD$$ трапеции $$ABCD$$ равны соответственно $$18$$ и $$30$$, а основание $$BC$$ равно $$3$$. Биссектриса угла $$ADC$$ проходит через середину стороны $$AB$$. Найдите площадь трапеции.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
1) Достроим $$DL$$ до пересечения с $$BC$$
$$DL\cap BC=M$$
2) $$\bigtriangleup MCD$$ - равнобедренный, т.к. $$\angle LDA=\angle LDC$$ ($$DL - (бисектрисса)
($$\angle BML=\angle ALD$$ - накрестлежащие)
3) $$CM=CD=30$$ $$\Rightarrow$$ $$BM=30-BC=27$$
4) $$\bigtriangleup MBL=\bigtriangleup LDA$$ ($$LB=LA$$; $$\angle MBL=\angle LAD$$; $$\angle MLB=\angle ALD$$)
$$\Rightarrow$$ $$AD=MB=27$$
5) опустим $$BH\perp CAD$$; $$CK\perp AD$$
$$BH=CK=y$$, тогда $$HK=KB=3$$
Пусть $$AH=x$$, тогда $$KD=27-x-3=24-x$$
Распишем т. Пифагора для $$\bigtriangleup ABH$$ и $$\bigtriangleup CKD$$
$$\left\{\begin{matrix}x^{2}+y^{2}=18^{2}\\(24-x)^{2}+y^{2}=30^{2}\end{matrix}\right.$$
$$(24-x)^{2}-x^{2}=30^{2}-18^{2}$$
$$576-48x+x^{2}-x^{2}=576$$
$$-48x=0$$
$$x=0$$ $$\Rightarrow$$
$$AB\perp AD$$
$$S_{ABCD}=\frac{3+27}{2}\cdot18=30\cdot9=270$$
Задание 672
Боковые стороны $$AB$$ и $$CD$$ трапеции $$ABCD$$ равны соответственно $$24$$ и $$26$$, а основание $$BC$$ равно $$8$$. Биссектриса угла $$ADC$$ проходит через середину стороны $$AB$$. Найдите площадь трапеции.
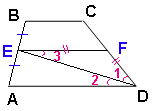BC = 8AB = 24
CD = 26 EF средняя линия. ∆EFD равнобедренный (∠1=∠2 по условию, ∠3=∠2 как накрест лежащие ⇒ ∠1=∠3)
EF = FD = CD/2 = 26 / 2 = 13 AD = 2 EF - BC = 26 - 8 18 Предположим, что AB ⊥ AD
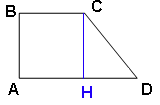CH² = 26² - (18 - 8)² = 676 - 100 576 = AB² ⇒ CH = AB
Предположение верно ⇒ Высота трапеции h = AB
$$S = \frac{AD + BC)}{2}\cdot h=\frac{18+8}{2}\cdot24=312$$
Задание 1533
Боковые стороны $$AB$$ и $$CD$$ трапеции $$ABCD$$ равны соответственно $$12$$ и $$13$$, а основание $$BC$$ равно $$4$$. Биссектриса угла $$ADC$$ проходит через середину стороны $$AB$$. Найдите площадь трапеции.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
