ОГЭ 2024. Вариант 8 Ященко 36 вариантов ФИПИ школе.
Решаем 8 вариант ОГЭ Ященко 2024 года сборника ФИПИ школе 36 вариантов. Полный разбор всего 8 варианта (всех заданий) Ященко 2024 ФИПИ 36 вариантов.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 1-5
Счетчики
В жилых домах установлены бытовые электросчётчики, которые фиксируют расход электроэнергии в киловатт-часах (кВт-ч). Учёт расхода электроэнергия может быть однотарифным, двухтарифным или трёхтарифным.
При однотарифном учёте стоимость 1 кВт·ч электроэнергии не меняется в течение суток. При двухтарифном и трёхтарифном учёте она различна в зависимости от времени суток (сутки разбиты на периоды, называемые тарифными зонами).
В таблице дана стоимость 1 кВт·ч электроэнергии в рублях в 2022 году.
| январь-июнь | июль-ноябрь | декабрь | |
| Однотарифный учет | 5,15 | 5,43 | 5,66 |
| Двухтарифный учет (распределение по двум тарифным зонам): | |||
| ночная зона Т1 (23.00-7.00) | 1,74 | 1,88 | 2,62 |
| дневная зона Т2 (7.00-23.00) | 5,92 | 6,24 | 6,91 |
| Трехтарифный учет (распределение по двум тарифным зонам): | |||
| ночная зона Т2 (23.00-7.00) | 1,74 | 1,88 | 2,62 |
| полупиковая зона Т3 (10.00-17.00; 21.00-23.00) | 5,15 | 5,43 | 5,66 |
| пиковая зона Т1 (7.00-10.00; 17.00-21.00) | 6,18 | 6,52 | 8,23 |
В квартире у Ивана Денисовича установлен трёхтарифный счётчик, и в 2022 году Иван Денисович оплачивал электроэнергию по трёхтарифному учёту.
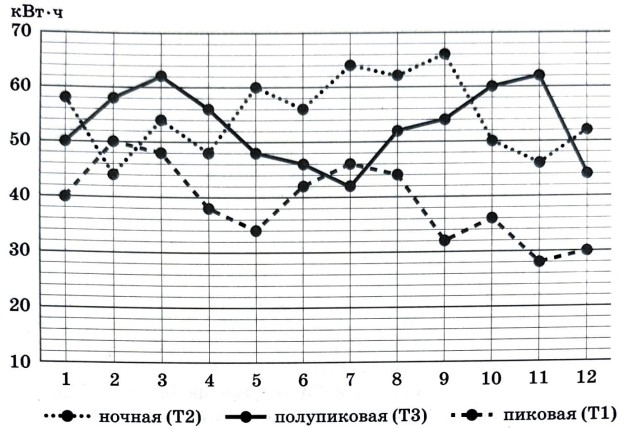
На рисунке точками показан расход электроэнергии в квартире Ивана Денисовича по тарифным зонам за каждый месяц 2022 года. Для наглядности точки соединены линиями.
1. Пользуясь рисунком, поставьте в соответствие каждому из указанных периодов времени характеристику расхода электроэнергии.
ПЕРИОДЫ
ХАРАКТЕРИСТИКИ
- расход в пиковой и ночной зонах уменьшился одинаково
- расход уменьшился во всех трёх тарифных зонах
- расход в пиковой зоне увеличился на столько же, на сколько уменьшился расход в полупиковой зоне
- расход в ночной зоне уменьшился, а в пиковой и полупиковой - увеличился
В таблице под каждой буквой укажите соответствующий номер.
| А | Б | В | Г |
2. Сколько кВт*ч было израсходовано в августе?
3. На сколько рублей больше заплатил бы Иван Денисович за электроэнергию, израсходованную в марте, если бы пользовался однотарифным учётом?
4. На сколько процентов общий расход электроэнергии в квартире Ивана Денисович в марте был больше, чем в апреле? Ответ округлите до десятых.
5. Сосед Ивана Денисовича, Илья Данилович, исходя из данных по расходу электроэнергии за 2022 год в своей квартире, рассчитал средний расход электроэнергии за месяц по тарифным зонам:
Илья Данилович предполагает, что в 2023 году средний расход электроэнергия будет таким же. Исходя из этого, выберите наиболее выгодный вариант учёта электроэнергии для Ильи Даниловича в 2023 году (однотарифный, двухтарифный или трёхтарифный). Считайте, что стоимость 1 кВт ч электроэнергии будет такой же, как в декабре 2022 года. Одените общие расходы Ильи Даниловича на оплату электроэнергии (в рублях) за 2023 год (по наиболее выгодному варианту учёта), если средний расход электроэнергии действительно будет таким же.
- менее 5 тыс. руб.
- от 5 тыс. руб. до 10 тыс. руб.
- от 10 тыс. руб. до 15 тыс. руб.
- от 15 тыс. руб. до 20 тыс. руб.
- от 20 тыс. руб. до 25 тыс. руб.
В ответ запишите номер верного варианта оценки расходов.
Задание 14
К концу $$2015$$ года в городе проживало $$62\ 000$$ человек. Каждый год число жителей города возрастало на одну и ту же величину. В конце $$2022$$ года в городе проживало $$69\ 070$$ человек. Какова была численность населения этого города к концу $$2018$$ года?
Задание 19
Какие из следующих утверждений верны?
- В прямоугольном треугольнике гипотенуза равна сумме катетов.
- Если в ромбе один из углов равен 90 градусам, то этот ромб является квадратом.
- Расстояние от точки, лежащей на окружности, до центра окружности равно радиусу.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
1) Перенесём всё в одну часть: $$x^4 - (3x - 10)^2 = 0,$$ $$(x^2 - (3x - 10))(x^2 + (3x - 10)) = 0,$$ $$(x^2 - 3x + 10)(x^2 + 3x - 10) = 0.$$
2) Решим квадратные уравнения.
Уравнение $$x^2 - 3x + 10 = 0.$$ Дискриминант: $$D = (-3)^2 - 4\cdot 1\cdot 10 = 9 - 40 = -31.$$ Действительных корней нет.
Уравнение $$x^2 + 3x - 10 = 0.$$ Дискриминант: $$D = 3^2 - 4\cdot 1\cdot(-10) = 9 + 40 = 49.$$ Корни: $$x_{1,2} = \dfrac{-3 \pm \sqrt{49}}{2\cdot 1} = \dfrac{-3 \pm 7}{2},$$ $$x_1 = 2,\quad x_2 = -5.$$
Задание 21
Из городов $$A$$ и $$B$$ навстречу друг другу одновременно выехали мотоциклист и велосипедист. Мотоциклист приехал в $$B$$ на $$36$$ минут раньше, чем велосипедист приехал в $$A$$, а встретились они через $$24$$ минуты после выезда. Сколько часов затратил на путь из $$B$$ в $$A$$ велосипедист?