Задание 2563
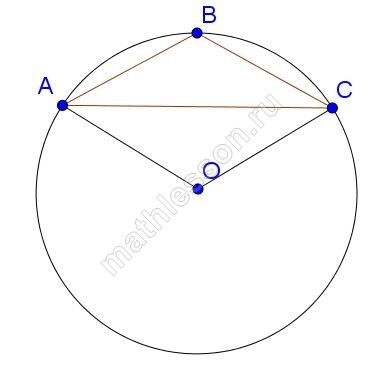
$$AC$$ и $$BD$$ — диаметры окружности с центром $$O$$. Угол $$AOD$$ равен $$44^\circ$$. Найдите градусную меру угла $$ACB$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 4906
Боковая сторона равнобедренного треугольника равна $$5$$. Угол при вершине, противолежащий основанию, равен $$120^\circ$$. Найдите диаметр окружности, описанной около этого треугольника.
Пусть угол B равен 120 градусам, тогда $$\smile AC = 240^{\circ}$$ (по свойству вписанного угла), тогда меньшая дуга CA равна $$360-240=120^{\circ}$$, и центральный угол, опирающийся на эту дугу так же составляет 120 градусов ($$\angle AOC$$). Так как треугольники ABC и ACO равнобедренные, имею общую сторону и равные углы против этой стороны, то они между собой равны, следовательно, AO=5=r, где r - радиус окружности, следовательно, диаметр окружности равен 10
Задание 2142
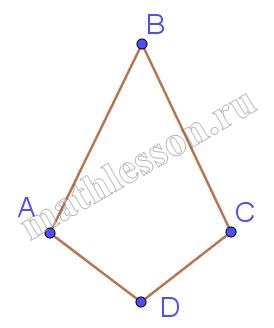
В выпуклом четырёхугольнике $$ABCD$$ известно, что $$AB = BC$$, $$AD = CD$$, $$\angle B = 77^\circ$$, $$\angle D = 141^\circ$$. Найдите градусную меру угла $$A$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 2479
В окружности с центром $$O$$ отрезки $$AC$$ и $$BD$$ — диаметры. Угол $$AOD$$ равен $$108^\circ$$. Найдите угол $$ACB$$. Ответ дайте в градусах.
Так как АС и BD — диаметры, то дуги AD=BC и AB=CD. Найдем градусную меру дуги AB, на которую опирается вписанный угол ACB. Так как угол AOD = 108°, то градусная мера дуги AD = 108° и тогда градусная мера:
$$AB=\frac{360^{\circ}-AD-BC}{2}=$$$$\frac{360^{\circ}-2\cdot 108^{\circ}}{2}=72^{\circ}$$
Так как угол ACB является вписанным, то он равен половине градусной меры дуги, на которую опирается, то есть:
$$\angle ACB=\frac{AB}{2}=\frac{72^{\circ}}{2}=36^{\circ}$$
Задание 782
В окружность вписан равносторонний восьмиугольник $$ABCDEFGH$$. Найдите градусную меру угла $$ACE$$.
Равные хорды отсекают равные дуги. Т.е. каждая сторона отсекает дугу $$\frac{360^{\circ}}{8}=45^{\circ}.$$
$$\angle ACE$$ опирается на дугу, отсекаемую 4 сторонами, т.е. $$180^{\circ},$$ но угол вписанный $$\Rightarrow\angle ACE=\frac{180^{\circ}}{2}=90^{\circ}$$
Задание 4909
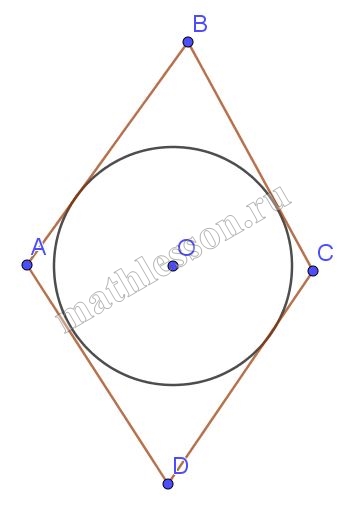
В параллелограмм вписана окружность. Найдите периметр параллелограмма, если одна из его сторон равна $$6$$.
Задание 2983
В трапецию, сумма длин боковых сторон которой равна $$12$$, вписана окружность. Найдите длину средней линии трапеции.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Если в четырехугольник можно вписать окружность, то суммы его противоположных сторон равны $$\Rightarrow$$ сумма оснований равна 12.Средняя линия равна полусумме оснований $$\Rightarrow$$ 6
Задание 3177
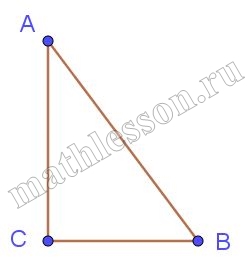
В треугольнике $$ABC$$ $$AC = \sqrt{5}$$, $$BC = \sqrt{11}$$, угол $$C = 90^\circ$$. Найдите радиус окружности, описанной около этого треугольника.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 4240
В треугольнике $$ABC$$ $$AC = 3\sqrt{7}$$, $$BC = 3\sqrt{2}$$, угол $$C$$ равен $$90^\circ$$. Найдите радиус окружности, описанной около этого треугольника.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Радиус описанной вокруг прямоугольного треугольника окружности равен половине длины его гипотенузы. Найдем гипотенузу по теореме Пифагора: $$AB=\sqrt{AC^{2}+BC^{2}}=\sqrt{9*7+9*2}=9$$ В таком случае радиус будет равен 9/2 = 4,5
Задание 3775
В треугольнике $$ABC$$ известно, что $$AC = 24$$, $$BC = \sqrt{265}$$, угол $$C = 90^\circ$$. Найдите радиус описанной окружности этого треугольника.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


По теореме Пифагора: $$AB=\sqrt{AC^{2}+BC^{2}}=\sqrt{576+265}=29$$. По свойству радиуса описанной окружности около прямоугольного треугольника : $$R=\frac{AB}{2}=14,5$$
Задание 2013
В треугольнике $$ABC$$ угол $$A$$ равен $$80^\circ$$, а угол $$B$$ равен $$40^\circ$$. Длина стороны $$AB$$ равна $$20\sqrt{3}$$. Найдите радиус окружности, описанной около треугольника $$ABC$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 2545
В угол $$C$$ величиной $$18^\circ$$ вписана окружность, которая касается сторон угла в точках $$A$$ и $$B$$, точка $$O$$ — центр окружности. Найдите градусную меру угла $$AOB$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 1198
В угол величиной $$70^\circ$$ вписана окружность, которая касается его сторон в точках $$A$$ и $$B$$. На большей из дуг $$AB$$ этой окружности выбрали точку $$C$$. Найдите градусную меру угла $$ACB$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 2182
Высота трапеции равна $$24$$. Найдите радиус окружности, вписанной в эту трапецию.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!