Окружности и их элементы
Задание 775
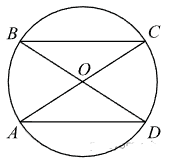
В окружности через середину $$O$$ хорды $$BD$$ проведена хорда $$AC$$ так, что дуги $$AB$$ и $$CD$$ равны. Докажите, что $$O$$ — середина хорды $$AC$$.
Задание 2952
Две окружности с радиусами $$R$$ и $$r$$ касаются друг друга внешним образом в точке $$A$$. Общие касательные $$AD$$ и $$BC$$ к окружностям пересекаются в точке $$D$$. Докажите, что $$AD^{2}=Rr$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


1) По свойству касательных : CD=DA и DA=DB $$\Rightarrow$$ $$CD=DB\Rightarrow$$ AD-медиана $$\Rightarrow$$$$\angle CAB=90$$
2) Пусть $$\angle ACD=\alpha \Rightarrow$$ из $$\Delta ABC$$: $$\angle ABC=90-\alpha$$. Из $$\Delta O_{1}CD$$: $$\angle CO_{1}D=\angle ACD=\alpha$$ и $$\angle AO_{1}D=\angle CO_{1}D=\alpha$$. Аналогично , $$\angle ABC=\angle DO_{2}B=\angle DO_{2}A=90-\alpha$$. Тогда $$\angle O_{1}DO_{2}$$( из $$\Delta O_{1}D0_{2}$$) равен 90 ($$180-(\alpha +90-\alpha)$$)
3) из $$\Delta O_{1}CD$$: $$O_{1}D^{2}=O_{1}C^{2}+CD^{2}=R^{2}+AD^{2}$$. Из $$\Delta O_{2}DB$$: $$O_{2}D=DB^{2}+O_{2}B^{2}=r^{2}+AD^{2}$$. При этом $$O_{1}D^{2}+O_{2}D^{2}=O_{1}O_{2}^{2}=(R+r)^{2}$$. Тогда: $$R^{2}+r^{2}+2AD^{2}=$$$$R^{2}+2Rr+r^{2}\Rightarrow$$ $$AD^{2}=Rr$$
Задание 4308
Докажите, что прямая, проходящая через точки пересечения двух окружностей, делит пополам общую касательную к ним
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


По свойству касательной и секущей: $$AM^{2}=MC\cdot MN$$
$$MB^{2}=MC\cdot MN$$
$$\Rightarrow$$ $$AM^{2}=MB^{2}$$
$$\Rightarrow$$ $$AM=MB$$
ч.т.д.
Задание 723
Окружности с центрами в точках $$P$$ и $$Q$$ не имеют общих точек, и ни одна из них не лежит внутри другой. Внутренняя общая касательная к этим окружностям делит отрезок, соединяющий их центры, в отношении $$m:n$$. Докажите, что диаметры этих окружностей относятся как $$m:n$$.
Задание 2681
Четыре точки окружности следуют в порядке $$A$$, $$B$$, $$C$$ и $$D$$. Продолжения хорды $$AB$$ за точку $$B$$ и хорды $$CD$$ за точку $$C$$ пересекаются в точке $$E$$, причем угол $$AED$$ равен $$60^{\circ}$$. Угол $$ABD$$ в три раза больше угла $$BAC$$. Докажите, что $$AD$$ – диаметр окружности.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!