Кусочно-непрерывные функции
Задание 3428
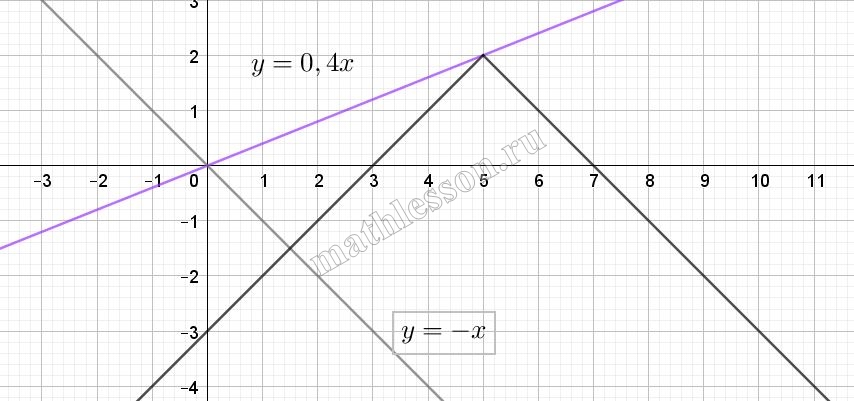
Найдите все значения $$k$$, при которых прямая $$y = kx$$ пересекает в двух точках ломаную, заданную условиями: $$y = \left\{\begin{aligned} x - 3,& x < 5 \\ 7 - x,& x \ge 5 \end{aligned}\right.$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


$$y=\left\{\begin{matrix}x-3, x<5 & & \\7-x, x\geq 5& &\end{matrix}\right.$$
Начертим график данной функции :
При a>0 до момента , когда пройдет поезд (5;2) (прямая розового цвета) : $$2=5*k\Rightarrow k=0,4$$, то есть $$k\in [0; 0,4)$$.
При a<0, пока не станет параллельна (прямая серого цвета) прямой y=7-x, то есть $$a\in (-1; 0)$$ Итог (-1; 0,4)
Задание 3934
Постройте график функции $$y = \begin{cases} -x^2 - 4x - 4,& x -1 \\ 1 - |x - 1|,& x \ge -1 \end{cases}$$ и определите, при каких значениях $$m$$ прямая $$y = m$$ имеет с графиком ровно две общие точки.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 332
Постройте график функции $$y = \left\{\begin{aligned} -x^2 + 2x + 3,& x \ge -1 \\ -x + 1,& x -1 \end{aligned}\right.$$. Определите, при каких значениях $$m$$ прямая $$y = m$$ имеет с графиком ровно две общие точки.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 3406
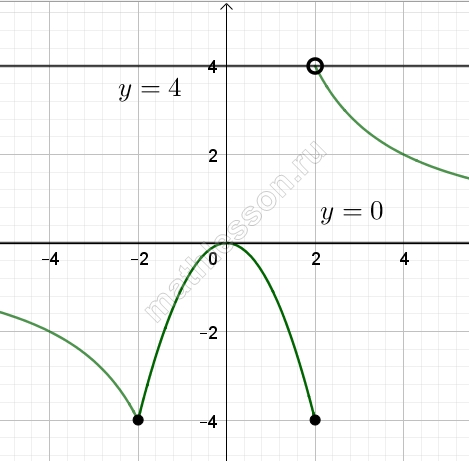
Постройте график функции $$y = \left\{\begin{aligned} -x^2, & |x| \leq 2 \\ \frac{8}{x}, & |x| > 2 \end{aligned}\right.$$ и определите, при каких значениях $$a$$ прямая $$y = ax$$ будет иметь с графиком единственную общую точку.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Начертим график данной функции $$y=\left\{\begin{matrix} -x^{2}, \left | x \right |\leq 2\\ \frac{8}{x}, \left | x \right |>0\end{matrix}\right.$$
Учтем, что график $$y=-x^{2}$$ при $$x\in [-2;2]$$ (на концах закрашенные точки, так как неравенство нестрогое), на остальной части область определения $$y=\frac{8}{x}$$.
$$y=a$$ - прямая, параллельная оси Ox, тогда одну точку будет иметь при $$a\in [0;4)$$
Задание 2338
Постройте график функции $$y = \left\{\begin{aligned} 2x - 2,& x 3 \\ -3x + 13{,}3,& 3 \le x \le 4 \\ 1{,}5x - 5,& x > 4 \end{aligned}\right.$$ и определите, при каких значениях $$m$$ прямая $$y = m$$ имеет с графиком ровно две общие точки.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 3194
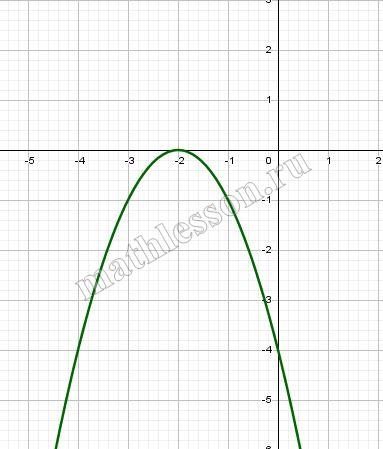
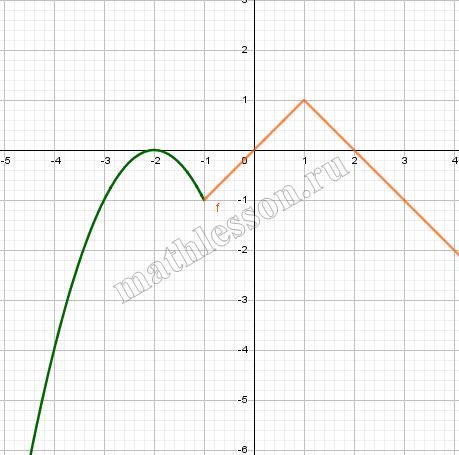
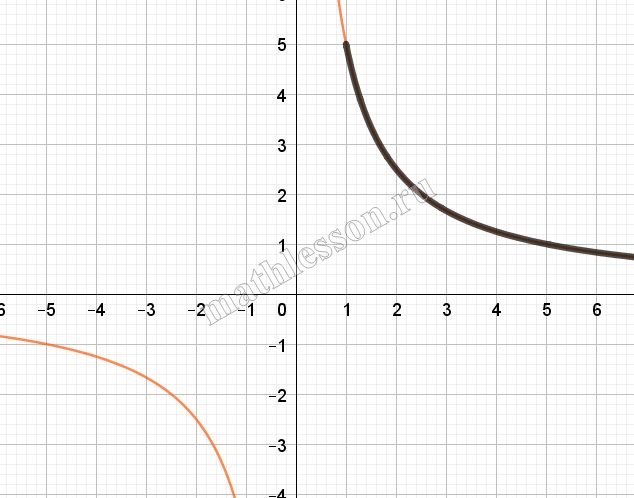
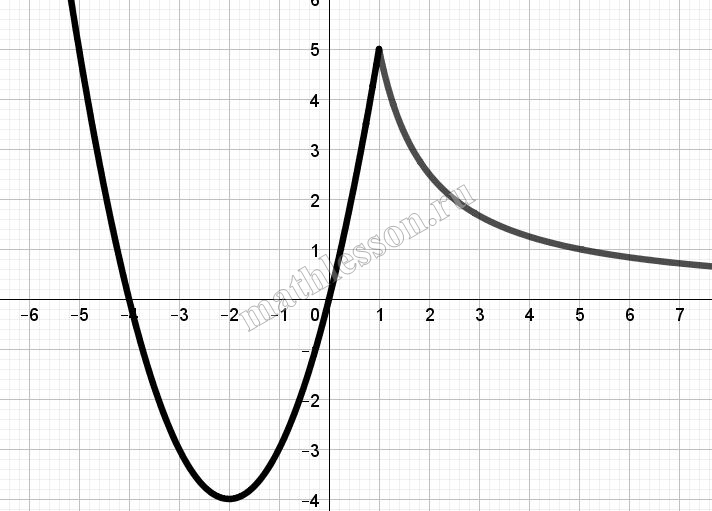
Постройте график функции $$y = \left\{\begin{aligned} x^2 + 4x, & x 1 \\ \frac{5}{x}, & x \geq 1 \end{aligned}\right.$$ и определите, при каких значениях $$a$$ прямая $$y = a$$ будет пересекать построенный график в трёх точках.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Рассмотрим $$y=x^{2}+4x$$. Найдем координаты вершины параболы: $$x_{0}=-\frac{4}{2}=-2$$; $$y_{0}=-4$$. Построим график функции с учетом ограничения по х (выделен черным)
Рассмотрим $$y=\frac{5}{x}$$ - это гипербола, расположенная в первой и третьей координатных четвертях. С учетом ограничениях по х (выделен черным):
Объединим полученные кусочные функции:
Прямая $$y=a$$ - прямая, параллелная оси Ох. Три точки пересечения будет при $$a \in (0;5)$$
Задание 1297
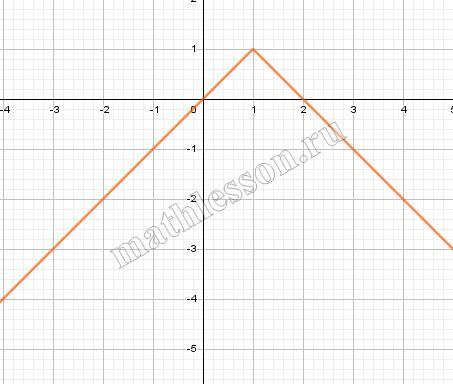
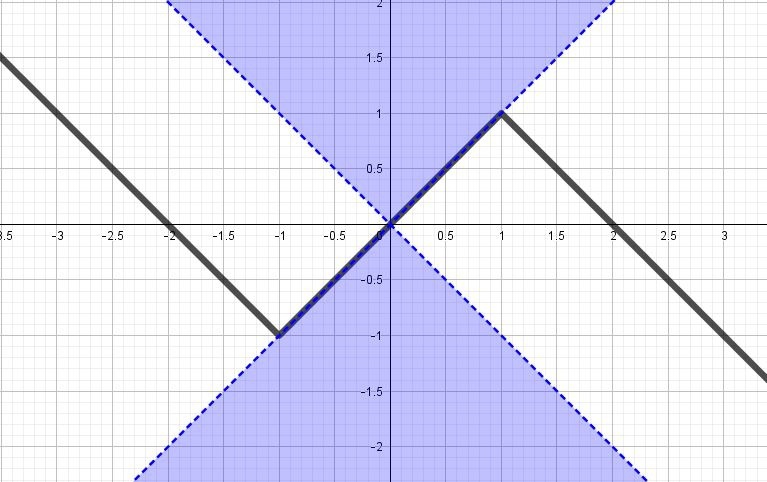
Постройте график функции $$y = |x + 1| - |x - 1| - x$$ и найдите все значения $$k$$, при каждом из которых прямая $$y = kx$$ имеет с графиком данной функции ровно одну общую точку.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


$$y=|x+1|-|x-1|-x$$
$$y=\left\{\begin{matrix} -x-1-(-x+1)-x,x\leq-1\\ x+1-(-x+1)-x,x\in(-1;1]\\ x+1-(x-1)-x,x>1 \end{matrix}\right.\Leftrightarrow y=\left\{\begin{matrix} -x-2,x\leq-1\\ x,x\in(-1;1]\\ -x+2,x>1 \end{matrix}\right.\Leftrightarrow$$
Ровно одну будет иметь при $$k>1$$ и $$k\in(-\infty;-1],$$ т.е. $$k\in (-\infty;-1]\cup(1;+\infty)$$
(на рисунке выделим зоны, где должен располагаться $$y=kx$$)