Задание 1297
Задание 1297
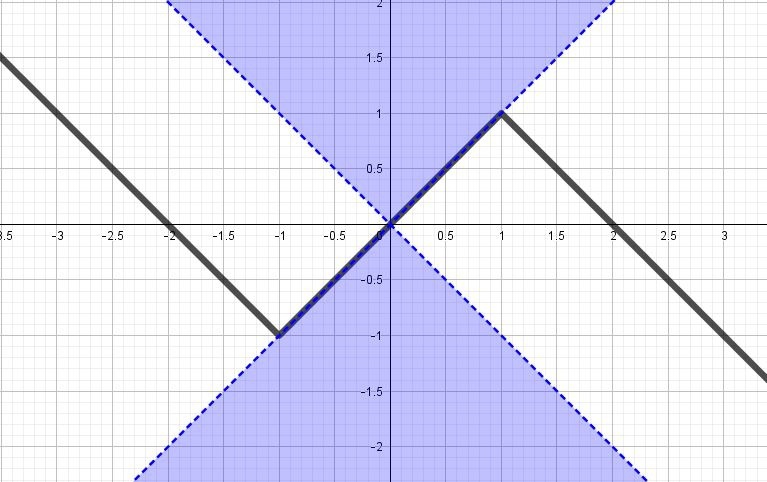
Постройте график функции $$y = |x + 1| - |x - 1| - x$$ и найдите все значения $$k$$, при каждом из которых прямая $$y = kx$$ имеет с графиком данной функции ровно одну общую точку.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


$$y=|x+1|-|x-1|-x$$
$$y=\left\{\begin{matrix} -x-1-(-x+1)-x,x\leq-1\\ x+1-(-x+1)-x,x\in(-1;1]\\ x+1-(x-1)-x,x>1 \end{matrix}\right.\Leftrightarrow y=\left\{\begin{matrix} -x-2,x\leq-1\\ x,x\in(-1;1]\\ -x+2,x>1 \end{matrix}\right.\Leftrightarrow$$
Ровно одну будет иметь при $$k>1$$ и $$k\in(-\infty;-1],$$ т.е. $$k\in (-\infty;-1]\cup(1;+\infty)$$
(на рисунке выделим зоны, где должен располагаться $$y=kx$$)
Задание 3745
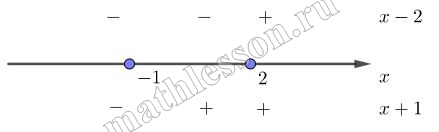
Постройте график функции $$y = |x - 2| - |x + 1|$$ и определите, при каких значениях $$k$$ прямая $$y = kx$$ имеет с графиком ровно три общие точки.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


$$y=\left | x -2 \right |-\left | x +1 \right |$$. Уберем модули. $$x -2=0$$ при $$x=2$$, а $$x+1=0$$, при х=-1$$. Отметим полученные точки на координатной прямой и посмотрим, какие значения принимают подмодульные выражения на различных промежутках:
Получили три интервала:
1)$$\left\{\begin{matrix}x \leq -1\\y=-x +2+x +1=3 \end{matrix}\right.$$
2)$$\left\{\begin{matrix} -1<x<2\\y=-x +2-x -1=-2*x +1\end{matrix}\right.$$
3)$$\left\{\begin{matrix}x \geq 2 \\y=x -2-x -1=-3 \end{matrix}\right.$$
Построим график с учетом полученных интервалов и их кусочных функций:
Графиком функции $$y=kx$$ является прямая, проходящая через начало координат. Очевидно, что для 2х пересечений прямая должна пройти через координату (2;-3).
Найдем коэффициент k:
$$-3=k*2\Leftrightarrow$$$$k=-1,5$$
Тогда, для 3х пересечений, коэффициент должен быть больше, чем -1,5, но меньше 0, то есть $$k \in(-1,5;0)$$
Задание 4236
Постройте график функции $$y = |x - 3| - |x + 3|$$ и найдите все значения $$k$$, при которых прямая $$y = kx$$ имеет с графиком данной функции ровно одну общую точку.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 3173
Постройте график функции $$y = |x - 4| + |x + 4|$$ и найдите все значения $$k$$, при которых прямая $$y = kx$$ имеет с графиком данной функции ровно одну общую точку.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Рассмотрим раскрытие модулей:
$$\left\{\begin{matrix}x\leq -4, y=-x+4-(-x-4)=8\\x \in (-4,4)(1), y =-x+4-(x+4)=-2x-8\\x\geq 4(2), y=x-4-(x+4)=-8(3)\end{matrix}\right.$$
Построим график данной кусочной функции:
Как видим, одна точка пересечения у графика будет в случае: $$k \in (-\infty ;-2)\cup [0;+\infty )$$

Задание 3243
Постройте график функции $$y = |x + 3| + |x - 3|$$ и найдите все значения $$a$$, при которых прямая $$y = ax + 6$$ имеет с графиком ровно две общие точки.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Раскроем модуль:
$$x\leq -3\Leftrightarrow y=-x-3-x+3=-2x$$
$$x \in (-3, 3]\Leftrightarrow y=x+3-x+3=6$$
$$x>3\Rightarrow y=x+3+x-3=2x$$
Начертим график:
Видим, что две точки пересечения будут в том случае, если прямая лежит в первой четверти при $$a\in(0;2)$$ (от момента, когда она будет параллельна оси Ох, до момента, когда она будет параллельна прямой $$y=2x$$) и, если прямая лежит во второй четверти при $$a\in(-2;0)$$ (от момента, когда она будет параллельна $$y=-2x$$, до момента, когда она будет параллельна оси Ох): $$a \in (-2;0)\cup (0;2)$$
Задание 982
Постройте график функции $$y = |x + 1| - |x - 1|$$. Определите, при каких значениях $$a$$ прямая $$y = ax$$ имеет с графиком ровно одну общую точку.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!