Задание 1415
Задание 1415
Прямая, параллельная основаниям трапеции $$ABCD$$, пересекает её боковые стороны $$AB$$ и $$CD$$ в точках $$E$$ и $$F$$ соответственно. Найдите длину отрезка $$EF$$, если $$AD=35$$, $$BC=21$$, $$CF:DF=5:2$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 1017
Прямая, параллельная основаниям трапеции $$ABCD$$, пересекает её боковые стороны $$AB$$ и $$CD$$ в точках $$E$$ и $$F$$ соответственно. Найдите длину отрезка $$EF$$, если $$AD=48$$, $$BC=16$$, $$CF:DF=5:3$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


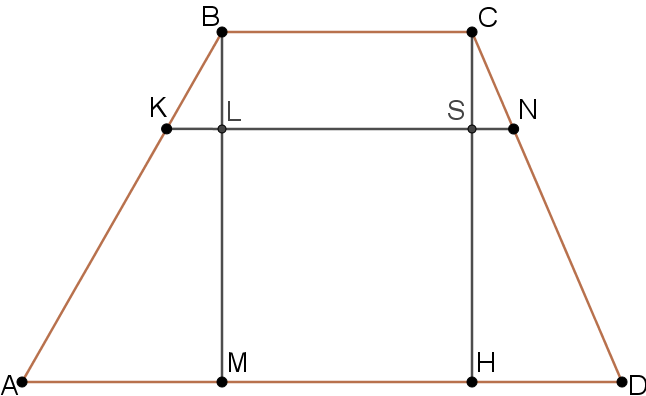
Задание 62
Прямая, параллельная основаниям трапеции $$ABCD$$, пересекает её боковые стороны $$AB$$ и $$CD$$ в точках $$K$$ и $$N$$ соответственно. Найдите длину отрезка $$KN$$, если $$AD = 40$$, $$BC = 16$$, $$CN = 12$$, $$ND = 18$$.
1) Проведём высоты: пусть $$CH \perp AD$$, $$BM \perp AD$$. Обозначим точки пересечения: $$CH \cap KN = S$$, $$BM \cap KN = L$$.
2) Так как $$KN \parallel AD$$, то углы $$\angle CNS = \angle CDH$$ (соответственные), а также $$\angle CSN = \angle CHD = 90^\circ$$. Следовательно, треугольники $$CNS$$ и $$CDH$$ подобны.
Длина стороны $$CD$$: $$CD = CN + ND = 12 + 18 = 30.$$ Из подобия: $$\frac{SN}{HD} = \frac{CN}{CD} = \frac{12}{30}.$$ Отсюда: $$SN = \frac{12}{30}\,HD.$$
3) Аналогично пункту 2: треугольники $$BKL$$ и $$BAM$$ подобны, поэтому $$KL = \frac{12}{30}\,AM.$$ Кроме того, выполняется равенство $$BC = LS = MH$$ (прямоугольники), а значит $$BC = LS = MH = 16.$$
4) Тогда $$AM + HD = AD - MH = 40 - 16 = 24.$$
5) Теперь длина отрезка $$KN$$: $$KN = KL + LS + SN = \frac{12}{30}(AM + HD) + 16 = \frac{12}{30}\cdot 24 + 16 = 9{,}6 + 16 = 25{,}6.$$
Ответ: $$25{,}6.$$
Задание 83
Прямая, параллельная основаниям трапеции $$ABCD$$, пересекает её боковые стороны $$AB$$ и $$CD$$ в точках $$K$$ и $$N$$ соответственно. Найдите длину отрезка $$KN$$, если $$AD = 45$$, $$BC = 15$$, $$CN = 12$$, $$ND = 18$$.
1) Проведём высоты: пусть $$CH \perp AD$$, $$BM \perp AD$$. Обозначим точки пересечения: $$CH \cap KN = S$$, $$BM \cap KN = L$$.
2) Так как $$KN \parallel AD$$, то углы $$\angle CNS = \angle CDH$$ (соответственные), а также $$\angle CSN = \angle CHD = 90^\circ$$. Следовательно, треугольники $$CNS$$ и $$CDH$$ подобны.
Из подобия: $$\frac{SN}{HD} = \frac{CN}{CD} = \frac{12}{30}.$$ Отсюда: $$SN = \frac{12}{30}\,HD.$$
3) Аналогично пункту 2: треугольники $$BKL$$ и $$BAM$$ подобны, поэтому $$KL = \frac{12}{30}\,AM.$$ Также выполняется равенство $$BL = CS$$ и $$BM = CH$$, отсюда $$\frac{BL}{BM} = \frac{CS}{CH} = \frac{CN}{CD}.$$
4) Так как $$BC = LS = MH = 15$$ (прямоугольники), то $$AM + HD = AD - MH = 45 - 15 = 30.$$
5) Тогда длина отрезка $$KN$$ равна $$KN = KL + LS + SN = \frac{12}{30}(AM + HD) + 15 =$$ $$\frac{12}{30}\cdot 30 + 15 = 12 + 15 = 27.$$