Задание 1929
Задание 1929
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


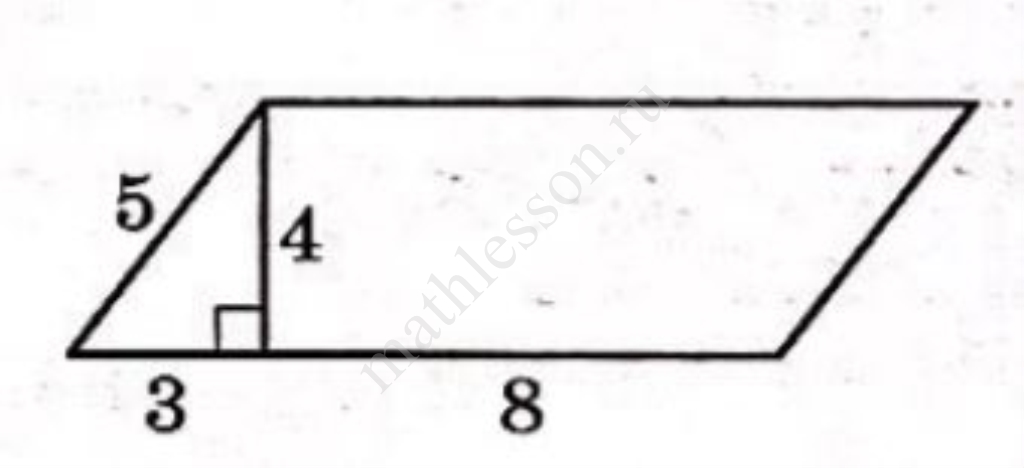
Площадь параллелограмма можно найти по формуле $$S=a\cdot h$$, где $$a$$ - длина стороны параллелограмма, $$h$$ - длина высоты, проведенной к этой стороне.
$$S=(3+5)\cdot 12=96$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


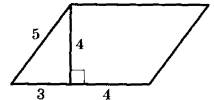
Сторона (a), к которой проведена высота равна $$3+4=7$$.
Площадь параллелограмма равна $$S=ah=7\cdot 4=28$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


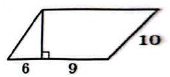
1) По рисунку основание параллелограмма равно $$a = 6 + 9 = 15,$$ а боковая сторона равна $$10.$$ Эта сторона вместе с отрезком основания длиной $$6$$ образует прямоугольный треугольник, поэтому высота параллелограмма — второй катет этого треугольника.
2) Найдём высоту из прямоугольного треугольника: $$h^2 + 6^2 = 10^2,$$ $$h^2 = 100 - 36 = 64,$$ $$h = 8.$$
3) Площадь параллелограмма: $$S = a \cdot h = 15 \cdot 8 = 120.$$
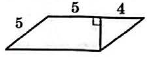
По рисунку длина нижнего основания равна сумме отрезков $$5$$ и $$4$$, то есть $$a = 5 + 4 = 9.$$ Правая боковая сторона образует с основанием прямоугольный треугольник с гипотенузой $$5$$ и одной из катетов $$4$$, значит высота параллелограмма равна второму катету.
1) Найдём высоту по теореме Пифагора: $$h^2 = 5^2 - 4^2 = 25 - 16 = 9,$$ $$h = 3.$$
2) Площадь параллелограмма: $$S = a\cdot h = 9\cdot 3 = 27.$$