Задание 84
Задание 84
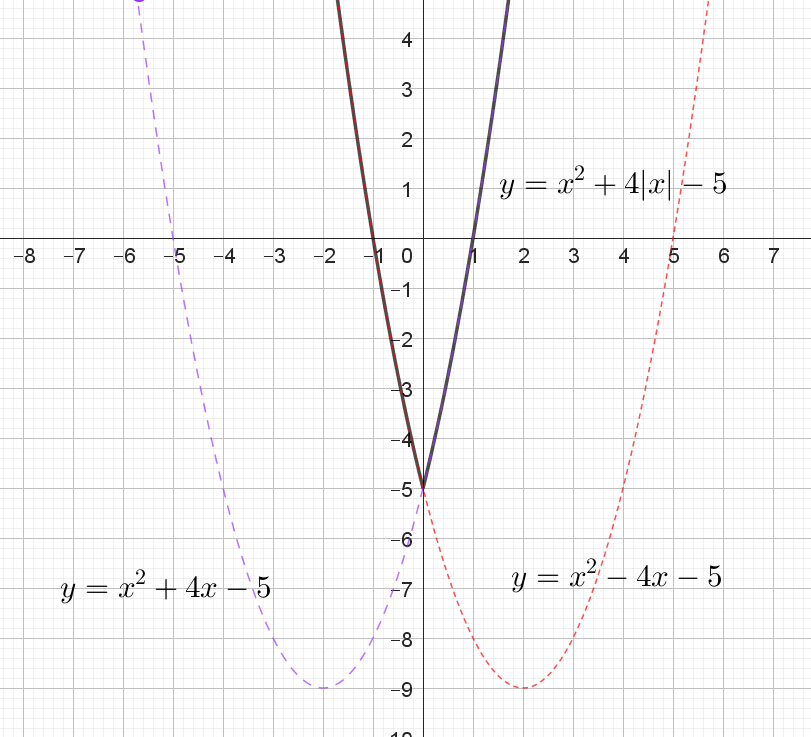
Постройте график функции $$y = x^2 + 4|x| - 5$$. Какое наибольшее число общих точек график данной функции может иметь с прямой, параллельной оси абсцисс?
1) Раскроем модуль по определениям:
При $$x \ge 0$$: $$y = x^2 + 4x - 5.$$ (на рисунке синим пунктиром) При $$x < 0$$: $$y = x^2 - 4x - 5.$$ (на рисунке красным пунктиром)
Это две параболы, открытые вверх. Первая имеет вершину при $$x = -2,$$ вторая — при $$x = 2,$$ обе вершины ниже точки пересечения при $$x = 0.$$ С учетом раскрытия модуля, на графике функции остаётся только правая ветвь первой параболы ($$y = x^2 + 4x - 5.$$ для $$x \ge 0$$) и левая ветвь второй параболы ($$y = x^2 - 4x - 5.$$ для $$x < 0$$).
2) Любая прямая, параллельная оси абсцисс, имеет уравнение $$y = k.$$ Она может пересечь левую ветвь графика не более чем в одной точке и правую ветвь — тоже не более чем в одной точке.
Значит, максимальное возможное число точек пересечения — две.
Задание 63
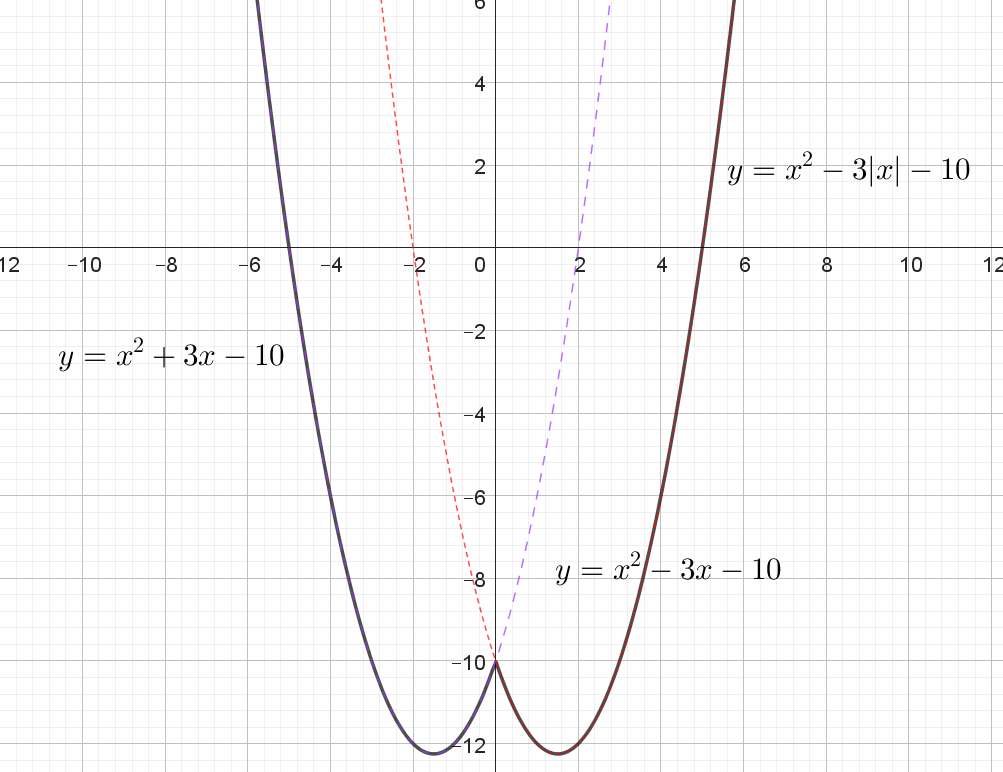
Постройте график функции $$y = x^2 - 3|x| - 10$$. Какое наибольшее число общих точек график данной функции может иметь с прямой, параллельной оси абсцисс?
1) Раскроем модуль:
При $$x \ge 0$$: $$y = x^2 - 3x - 10.$$ (красный пунктир) При $$x < 0$$: $$y = x^2 + 3x - 10$$ (синий пунктир).
Это две параболы, открытые вверх.
Первая имеет вершину при $$x = \frac{3}{2},$$ вторая — при $$x = -\frac{3}{2}.$$ Обе вершины принадлежат своим областям: первая — к $$x \ge 0,$$ вторая — к $$x < 0.$$ Поэтому на графике функции каждая парабола присутствует почти целиком (обрезана только по другую сторону от нуля).
2) Горизонтальная прямая $$y = k$$ может пересекать каждую параболу максимум в двух точках. Для значений $$k$$, лежащих выше обеих вершин (достаточно взять $$k$$ больше наибольшего из минимальных значений функций), прямая пересечёт каждую параболу в двух точках.
Следовательно, всего возможны четыре точки пересечения.