Задание 513
Аналоги к этому заданию:
Задание 781
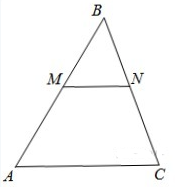
Прямая, параллельная стороне $$AC$$ треугольника $$ABC$$, пересекает стороны $$AB$$ и $$BC$$ в точках $$M$$ и $$N$$ соответственно, $$AC = 16$$, $$MN = 12$$. Площадь треугольника $$ABC$$ равна $$80$$. Найдите площадь треугольника $$MBN$$.
Ответ: 45
Скрыть
Треугольники MBN и АВС подобны, так как MN параллельна АС.
Из подобия:
$$\frac{MN}{AC}=\frac{12}{16}=\frac{3}{4}.$$ Это коэффициент подобия.
Площади подобных треугольников относятся как квадрат коэффициента подобия, то есть
$$\frac{S_{mbn}}{S_{abc}}=\frac{9}{16}.$$
Тогда $$S_{mbn}=\frac{9}{16}\cdot S_{abc}$$
$$S_{mbn}=\frac{9}{16}\cdot80=45$$