Задание 3166
Задание 3166
Постройте график функции $$y = \frac{2|x| - 1}{|x| - 2x^2}$$ и определите, при каких значениях $$k$$ прямая $$y = kx$$ не имеет с графиком ни одной общей точки.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


ОДЗ: $$\left | x \right |-2x^{2}\neq 0\Leftrightarrow$$ $$\left | x \right |-2\left | x \right |^{2} \neq 0\Leftrightarrow$$ $$\left | x \right |(1-2\left | x \right |)\neq 0\Leftrightarrow$$ $$\left\{\begin{matrix}x\neq 0\\ x\neq 0,5\\ x\neq -0,5\end{matrix}\right.$$.
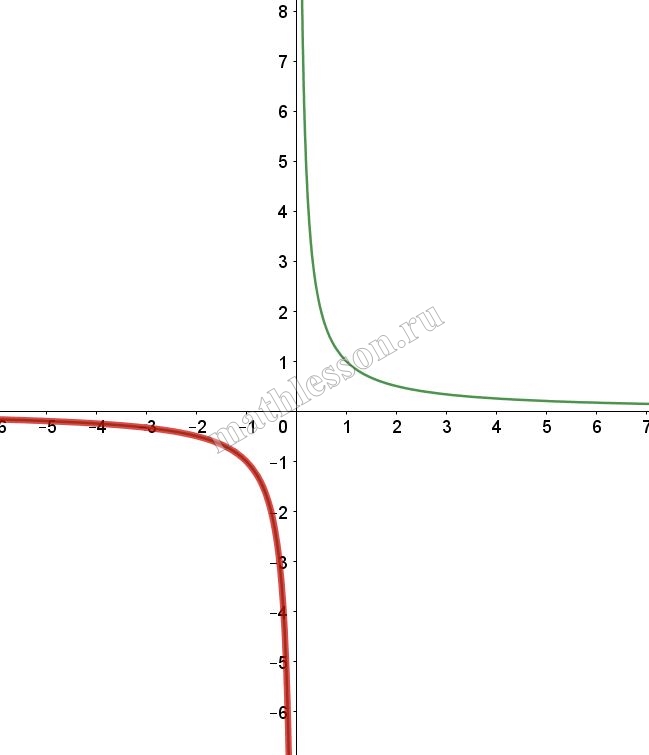
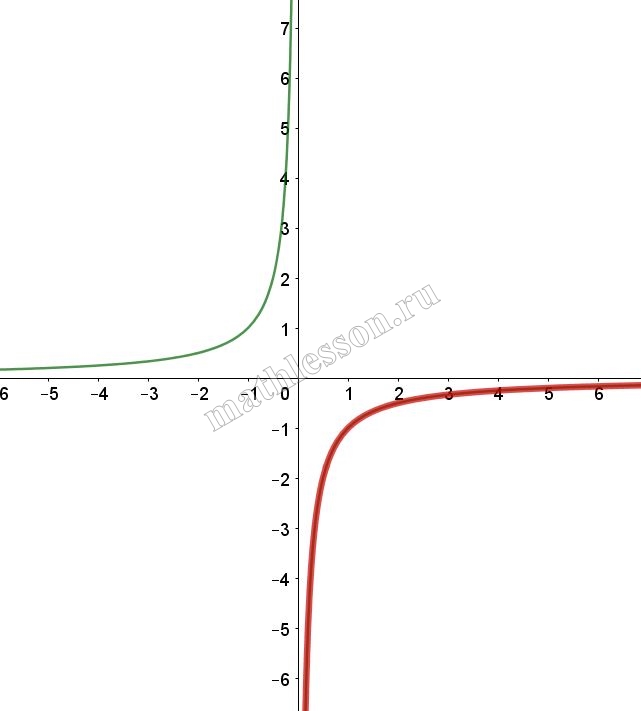
При $$x>0$$: $$y=\frac{2x-1}{x(1-2x)}=-\frac{1}{x}$$ (выдерена красным)
При $$x<0$$: $$y=\frac{-2x-1}{-x-2x^{2}}=\frac{1}{x}$$(выделена красным)
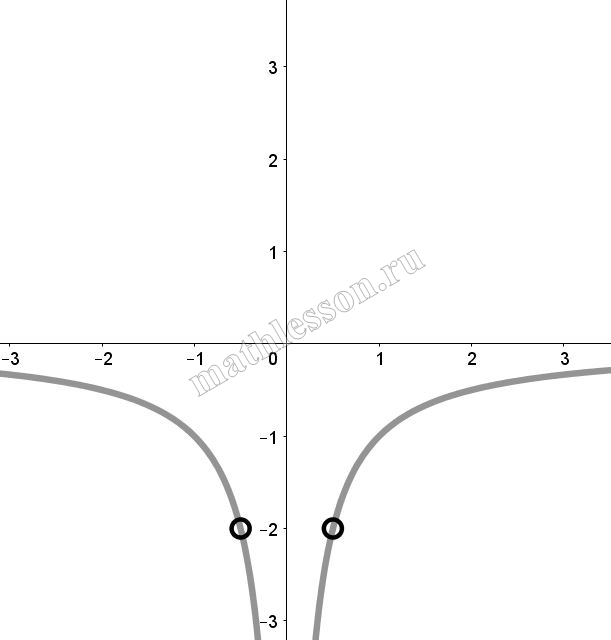
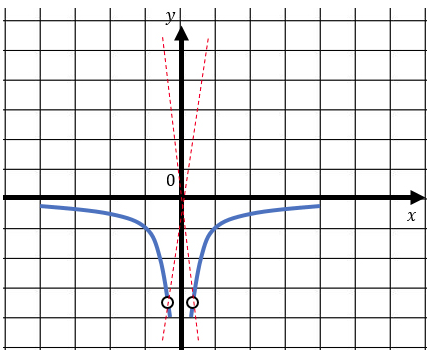
Итоговый график с учетом ОДЗ:
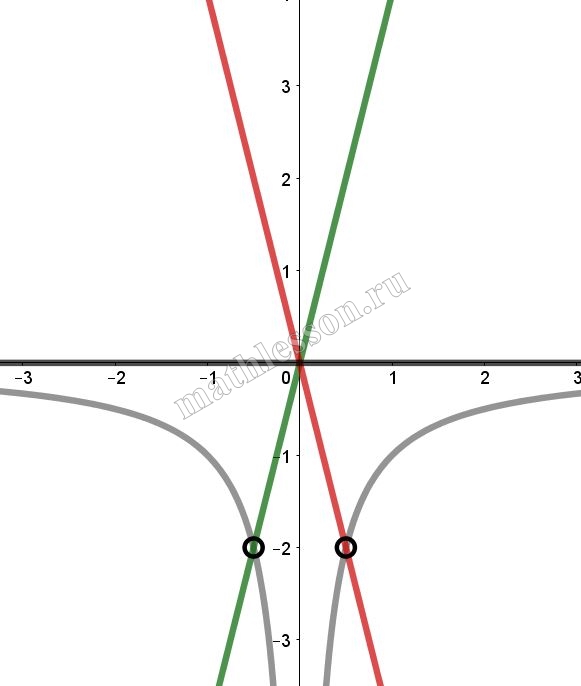
Найдем k: $$y=kx$$ проходит через (-0,5 ; -2): $$-2=-0,5*k\Rightarrow k=4$$(зеленая) и через (0,5; -2): $$-2=0,5k\Rightarrow k=-4$$(красная). При k=0 (черная) тоже не имеет пересечений
Задание 1793
Постройте график функции $$y = \frac{4{,}5|x| - 1}{|x| - 4{,}5x^2}$$. Определите, при каких значениях прямая $$y = ax$$ не имеет с графиком функции общих точек.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 1876
Постройте график функции $$y = \frac{|x| - 1}{|x| - x^2}$$ и определите, при каких значениях $$k$$ прямая $$y = kx$$ не имеет с графиком общих точек.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 2367
Постройте график функции $$y = \frac{|x| - 4}{x^2 - 4|x|}$$. Определите, при каких значениях $$p$$ прямая $$y = px$$ не имеет с графиком функции общих точек.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 658
Постройте график функции $$y = \frac{3{,}5|x| - 1}{|x| - 3{,}5x^2}$$. Определите, при каких значениях $$a$$ прямая $$y = ax$$ не имеет с графиком этой функции общих точек.
$$x = 0$$ – критическая точка, в ней подмодульное выражение меняет знак. Поэтому будем рассматривать два случая: когда $$x > 0$$ и $$x < 0$$.
1) При $$x > 0$$ функция примет такой вид
$$y=\frac{3,5x-1}{x-3,5x^2}=\frac{3,5x-1}{-x(-1+3,5x)}=-\frac{1}{x}$$
Графиком данной функции будет гипербола, к тому же, сразу определимся с ОДЗ. Т.к. у нас дана дробь, то ее знаменатель не может равняться нулю. Поэтому, икс не должен равняться 0 и 2/7 (х ≠ 0 и х ≠ 2/7).
Сразу найдем координаты точек, по которым будем чертить график.
| х | 0,5 | 1 | 2 |
| у | -2 | -1 | -0,5 |
Найдем координаты выколотой точки: если x ≠ 2/7, то y ≠ -3,5.
2) При $$х < 0$$ функция примет вид
$$y=\frac{-3,5x-1}{-x-3,5x^2}=\frac{-3,5x-1}{x(-1-3,5x)}=\frac{1}{x}$$
ОДЗ: х ≠ 0 и х ≠ -2/7.
Найдем координаты точек.
| х | -0,5 | -1 | -2 |
| у | -2 | -1 | -0,5 |
Найдем координаты выколотой точки: если x ≠ -2/7, то y ≠ -3,5.
3) Теперь можно чертить график (синие кусочки гипербол).
$$y = kx$$ – прямая, проходящая под наклоном через начало координат (k – угловой коэффициент). И есть две потенциальные прямые, которые с нашим графиком не имеют общих точек (на координатной плоскости они отмечены красным цветом). Осталось лишь найти чему равен коэффициент k.
Обе прямые непременно должны проходить через выколотые точки. И логично предположить, что чтобы найти k надо в уравнение $$y = kx$$ подставить координаты этих выколотых точек. Это мы сейчас и сделаем.
Для точки (-2/7; -3,5)
$$-\frac{7}{2}=-\frac{2}{7}k;\; k=\frac{49}{4}=12,25$$
Для точки (2/7; -3,5)
$$-\frac{7}{2}=\frac{2}{7}k;\; k=-\frac{49}{4}=-12,25$$
И не стоит забывать, что при $$k = 0$$ прямая $$y = kx$$ превращается в прямую $$y = 0$$, которая совпадает с осью Ох. А, как известно, гипербола ее никогда не пересечет.
Таким образом, при $$k = ±12,25$$ и $$k = 0$$ прямая $$y = kx$$ не имеет с графиком общих точек.