Задание 1534
Задание 1534
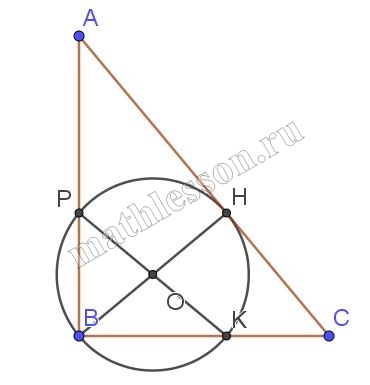
Точка $$H$$ является основанием высоты $$BH$$, проведённой из вершины прямого угла $$B$$ прямоугольного треугольника $$ABC$$. Окружность с диаметром $$BH$$ пересекает стороны $$AB$$ и $$CB$$ в точках $$P$$ и $$K$$ соответственно. Найдите $$BH$$, если $$PK=11$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Аналоги к этому заданию:
Задание 3193
Точка $$H$$ является основанием высоты $$BH$$, проведённой из вершины прямого угла $$B$$ прямоугольного треугольника $$ABC$$. Окружность с диаметром $$BH$$ пересекает стороны $$AB$$ и $$CB$$ в точках $$P$$ и $$K$$ соответственно. Найдите $$PK$$, если $$BH=12$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Рассмотрим $$\Delta PBK$$: $$\angle B=90\Rightarrow$$ PK-диаметр описанной окружности $$\Rightarrow PK=BH=12$$
Задание 1551
Точка $$H$$ является основанием высоты $$BH$$, проведённой из вершины прямого угла $$B$$ прямоугольного треугольника $$ABC$$. Окружность с диаметром $$BH$$ пересекает стороны $$AB$$ и $$CB$$ в точках $$P$$ и $$K$$ соответственно. Найдите $$BH$$, если $$PK=13$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
