Задание 1920
Задание 1920
В параллелограмме $$ABCD$$ проведена диагональ $$AC$$. Точка $$O$$ является центром окружности, вписанной в треугольник $$ABC$$. Расстояния от точки $$O$$ до точки $$A$$ и прямых $$AD$$ и $$AC$$ соответственно равны $$25$$, $$13$$ и $$7$$. Найдите площадь параллелограмма $$ABCD$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Аналоги к этому заданию:
Задание 637
В параллелограмме $$ABCD$$ проведена диагональ $$AC$$. Точка $$O$$ является центром окружности, вписанной в треугольник $$ABC$$. Расстояния от точки $$O$$ до точки $$A$$ и прямых $$AD$$ и $$AC$$ соответственно равны $$10$$, $$8$$ и $$6$$. Найдите площадь параллелограмма $$ABCD$$.
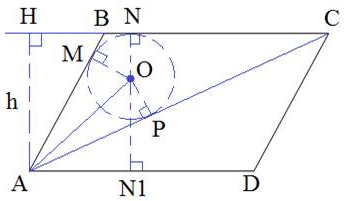
Окружность вписана в треугольник ABC с радиусами $$OM=ON=OP$$ и перпендикулярными сторонам AB, BC, AC соответственно. По теореме об отрезках касательных, имеем:
$$MB=BN, AM=AP, CN=CP$$.
Пусть $$BM=BN=x$$, а $$CN=CP=y$$. Тогда $$BC=AD=x+y$$. Отрезок $$NN_1=AH=8+6=14$$. Рассмотрим прямоугольный треугольник AMO. По теореме Пифагора найдем сторону AM:
$$AM=\sqrt{AO^2-OM^2}=\sqrt{10^2-6^2}=8$$
Значит, $$AP=AM=8$$. Найдем величину $$x+y$$ из формулы площади треугольника ABC:
$$S_{ABC}=\frac{1}{2}(x+y)\cdot14$$
Эту же площадь можно вычислить как
$$S_{ABC}=p\cdot r$$,
где $$p=\frac{1}{2}\cdot(AB+BC+AC)=8+x+y$$ - полупериметр треугольника ABC; $$r=6$$ – радиус вписанной окружности. Приравниваем площади, получаем уравнение:
$$7\cdot(x+y)=(x+y+8)\cdot6$$
$$7(x+y)-6(x+y)=48$$
$$x+y=48$$
Значит, $$BC=AD=48$$ и площадь параллелограмма, равна:
$$S_{ABCD}=AD\cdot H=48\cdot14=672$$